Ripple Constraint Design
- Updated2025-10-10
- 3 minute(s) read
A ripple constraint guarantees that the maximum error magnitude between the frequency response of the designed filter and the expected frequency response is equal to or below the constraint.
You might want to design filters with ripple constraints in the following situations:
- You want to specify the filter order and constrain the ripple magnitude in certain bands.
- You want to constrain all bands, and you want the DFD Remez Design VI to determine the minimum filter order that satisfies the requirements.
- You want to constrain all bands and specify the filter order as well. The DFD Remez Design VI reports an error if the constraints cannot be met. Otherwise, the DFD Remez Design VI returns a valid design with the ripple ratios among different bands the same as the ratios of the ripple constraints.
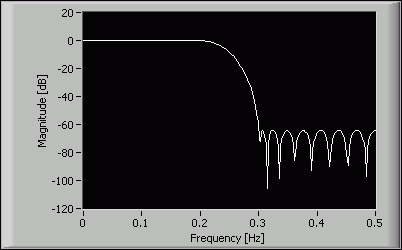
As an example for the first situation, suppose you want to design a 15th order lowpass filter, and you want the passband ripple magnitude to be no more than 0.1. You can set the passband frequency range to [0, 0.2] and the stopband frequency range to [0.3, 0.5] and apply equal weights in both bands. The following figure shows the magnitude response of the designed filter:

Notice that the passband ripple is much smaller than the requirement. To make the passband ripple just touch the upper constraint, you can reduce the initial weight in the passband to [0.01, 0.01] and run the VI again. The following figure shows the magnitude response of the redesigned filter:

The smaller weight value allows the DFD Remez Design VI to design a filter with a passband ripple that initially exceeds the constraint and then automatically adjust the weight level iteratively until the constraint is met.
As an example for the second situation, suppose you want to design a lowpass filter with the same passband and stopband frequency ranges as the previous example. You can specify the ripple constraints for the passband and the stopband as 0.01 and 0.001, respectively, and set the minimum order input to minEven. The following figure shows the magnitude response of the 28th order equi-ripple FIR filter that the DFD Remez Design VI returns: