You can use exact gain control to constrain the amplitude response of the filter to particular values at particular frequencies.

When you enter bands into the band specs input, the DFD Remez Design VI uses complex or magnitude approximation to create the design of the filter.

To use exact gain control in the DFD Remez Design VI, enter in the freqs of exact gain input a list of frequencies that you want to constrain to ideal amplitudes. If you also specify those frequencies in the band specs input, the DFD Remez Design VI uses the corresponding amplitudes. If you do not enter those frequencies in the band specs input, the DFD Remez Design VI interpolates the amplitudes linearly.

Consider a filter that has the same magnitude response as the filter in the Single-Point Band Design section. You can achieve sharper notches by applying exact gain control at 0.15 Hz and 0.35 Hz. By entering those single-point band frequency points in the freqs of exact gain input, the redesigned notch filter has a magnitude response as shown in the following figure:

Figure 40. Redesigned Notch Filter Magnitude Response with Exact Gain Control at 0.15 Hz and 0.35 Hz

Notice that the graph has sharper notches than the notch filter in the Single-Point Band Design section.

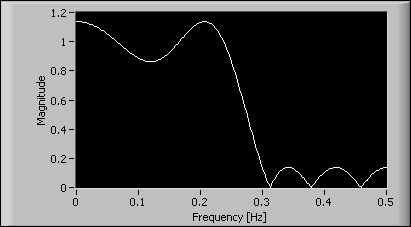
The following figure shows the magnitude response of a 12th order lowpass equi-ripple filter without any exact gain frequencies. The passband range is [0, 0.25] and the stopband range is [0.3, 0.5] with equal weights in both bands. Notice that the gain at DC, or the magnitude response at 0 Hz, is not exactly one.

Figure 41. 12th Order Lowpass Equi-Ripple Filter Magnitude Response Without Exact Gain Frequencies

If you want to force the gain to one at DC, enter 0 into the freqs of exact gain input and run the VI again. The following figure shows the magnitude response of the resulting filter:

Figure 42. Magnitude Response of 1212 Order Lowpass Equi-Ripple Filter with DC Gain Forced to One

Notice that the DC gain becomes exactly one without any noticeable ripple size increase.

The following figure shows the magnitude response of a 12th order highpass filter with a stopband frequency range of [0, 0.2] and a passband frequency range of [0.3, 0.5]:

Figure 43. 12th Order Highpass Filter Magnitude Response with Stopband [0, 0.2] and Passband [0.3, 0.5]

The signal is relatively clean except for a noise component at 0.1 Hz and the second harmonic at 0.2 Hz. To attenuate the noise power at those frequencies, you can enter 0.1 and 0.2 into the freqs of exact gain input.

The following figure shows the magnitude response of the filter with exact gains specified at 0.1 Hz and 0.2 Hz. Notice that the magnitude response at 0.1 Hz and 0.2 Hz is exactly zero.

Figure 44. Magnitude Response of Filter with Exact Gains at 0.1 Hz and 0.2 Hz, Resulting in Zero Gain at These Frequencies