Determines all zeros of a 1D function in a given interval. You must manually select the polymorphic instance to use.


icon

Inputs/Outputs

  • cdbl.png accuracy —

    accuracy controls the accuracy of the zeros and the extrema. The default is 1.00E-8.

  • cu16.png step type —

    step type controls the spacing used for the function values.

    In general, modified function leads to more accurate zeros and extrema.

    0fixed function (default)—Represents uniformly spaced function values.
    1modified function—Represents the optimal step size.
  • cu16.png algorithm —

    algorithm is the method used by the VI.

    0Ridders (default)
    1Newton Raphson
  • cdbl.png start —

    start is the start point of the interval. The default is 0.0.

  • cdbl.png end —

    end is the end point of the interval. The default is 1.0.

  • cstr.png formula —

    formula is a string describing the function. The formula can contain any number of valid variables.

  • i1ddbl.png Zeros —

    Zeros are the determined zeros of formula.

  • i1ddbl.png f(Zeros) —

    f(Zeros) contains the function values of Zeros.

    Usually, these values are close to 0.

  • iu32.png ticks —

    ticks is the time in milliseconds for the whole calculation.

  • ii32.png error —

    error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

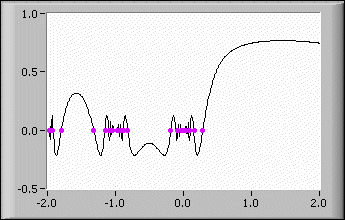
    • To obtain the zeros of sin(sinc(gamma(x))) in the interval (–2, 2), enter the following values on the front panel:

    • start: -2.00
    • end: 2.00
    • formula: sin(sinc(gamma(x)))

    The following illustration shows the graph and the zeros of sin(sinc(gamma(x))) in the interval (–2, 2).

    Note For some functions, Zeros may contain false zeros that are actually singularities. For true zeros, f(Zeros) is close to 0.

    Examples

    Refer to the following example files included with LabVIEW.

    • labview\examples\Mathematics\Optimization\1D Explorer.vi