Führt eine zweidimensionale Interpolation mithilfe einer ausgewählten Interpolationsmethode basierend auf der durch X, Y und Z definierten Zuordnungstabelle durch, wobei Z ein 2D-Array ist. Die polymorphe Instanz muss manuell ausgewählt werden.

Hinweis

Führt eine zweidimensionale Interpolation durch, wenn X, Y, xi und yi 1D-Arrays sind.


icon

Ein-/Ausgänge

  • ci32.png Methode —

    Methode gibt das Interpolationsverfahren an.

    0Nächstgelegen—Wählt den Z-Wert aus, der zu X und Y gehört und dem aktuellen xi- und yi-Wert am nächsten ist. Der interpolierte Wert wird auf den nächsten Datenpunkt gesetzt.
    1Bilinear—Setzt die interpolierten Werte auf Punkte entlang der Strecke zwischen X und Y.
    2Bikubisch—Erzeugt einen interpolierten Punkt auf einer bikubischen Oberfläche, wobei 16 der nächstgelegenen X-, Y- und Z-Werte berücksichtigt werden. Dadurch wird gewährleistet, dass die ersten partiellen Ableitungen und die gemischte Ableitung zweiter Ordnung der interpolierten Oberflächen stetig sind.
    3Spline (bikubisch)—Gewährleistet, dass die erste und zweite partielle Ableitung der kubischen Interpolationspolynome stetig sind, selbst an den Datenpunkten.
  • c2ddbl.png Z —

    Z ist das 2D-Array mit den Werten der abhängigen Variablen.

  • c1ddbl.png X —

    X ist das 1D-Array aus den Werten der ersten unabhängigen Variablen. X muss für alle Interpolationsarten monoton sein.

    Wenn X nicht leer ist, muss die Länge von X gleich der Anzahl der Spalten in Z sein. Wenn X leer ist, behandelt dieses VI X als [0, 1, …, N – 1], wobei N die Anzahl der Spalten in Z ist.

  • c1ddbl.png Y —

    Y ist das 1D-Array aus den Werten der zweiten unabhängigen Variablen. Y muss für alle Interpolationsarten monoton sein.

    Wenn Y nicht leer ist, muss die Länge von Y gleich der Anzahl der Zeilen in Z sein. Wenn Y leer ist, behandelt dieses VI Y als [0, 1, …, M – 1], wobei M die Anzahl der Zeilen in Z ist.

  • c1ddbl.png xi —

    xi ist ein 1D-Array aus Werten der ersten unabhängigen Variable, bei der interpolierte Werte der abhängigen Variable zi zu berechnen sind.

  • c1ddbl.png yi —

    yi ist ein 1D-Array aus Werten der zweiten unabhängigen Variable, bei der interpolierte Werte der abhängigen Variable zi zu berechnen sind.

  • ci32.png n Mal —

    n Mal bestimmt die Position der Interpolationspunkte. Interpolationen zwischen jedem X- und Y-Element werden n Mal wiederholt. Wenn Sie Daten mit xi oder yi verbinden, ignoriert dieses VI n Mal.

  • i2ddbl.png zi —

    zi ist das zweidimensionale Ausgangs-Array interpolierter Werte entsprechend der von xi, yi unabhängigen Variablenwerte.

  • i2ddbl.png xi verwendet —

    xi verwendet ist ein 2D-Array aus Werten der ersten unabhängigen Variable, bei der interpolierte Werte der abhängigen Variable zi zu berechnen sind.

    Wenn Sie Daten mit xi verbinden, gibt xi verwendet xi aus. Anderenfalls gibt xi verwendet ein Array mit Zeilen von 2n Mal – 1 gleichmäßig zwischen benachbarten Elementen in der ersten Zeile von X verteilten Punkten aus. Die Anzahl der Zeilen in xi verwendet entspricht der Anzahl der Zeilen in yi verwendet.

  • i2ddbl.png yi verwendet —

    yi verwendet ist ein 2D-Array aus Werten der zweiten unabhängigen Variable, bei der interpolierte Werte der abhängigen Variable zi zu berechnen sind.

    Wenn Sie Daten mit yi verbinden, gibt yi verwendet yi aus. Anderenfalls gibt yi verwendet ein Array mit Spalten von 2n Mal – 1 gleichmäßig zwischen benachbarten Elementen in Y verteilten Punkten aus. Die Spalten der Zeilen in yi verwendet entspricht der Anzahl der Spalten in xi verwendet.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Dieses VI arbeitet mit den unabhängigen Variablen X und Y sowie der abhängigen Variable Z in Tabellenform und gibt die interpolierten Werte zi zu jeder xi- und yi-Position aus. Das VI sucht in X und Y nach jedem Wert von xi bzw. yi und ermittelt anschließend anhand der relativen Position in X und Y den interpolierten Wert zi an der gleichen relativen Position in Z.

    Dieses VI hat vier verschiedene Interpolationsmethoden zur Auswahl.

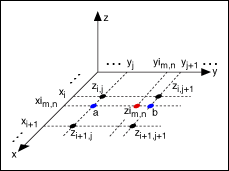
    Die folgende Abbildung zeigt xi und yi als 2D-Arrays, die die zu interpolierenden Koordinaten angeben. Die Koordinaten von zim, n sind also (xim, n, yim, n), wobei m und n die Indizes für xi, yi und zi sind. X und Y sind 1D-Arrays, die die Koordinaten von Z angeben. i und j sind die Indizes von X und Y. Z ist das 2D-Array, das die entsprechende abhängige Variable darstellt. Der rote Punkt kennzeichnet die Position von zim, n.

    Methode des naheliegendsten Werts

    Bei der Methode des nächstgelegenen Werts wird nach dem Wert gesucht, der (xim, n, yim, n) am nächsten liegt. Dann wird der dazugehörige z-Wert in Z zim, n zugeordnet. In der vorigen Abbildung ist zim, n = zi, j + 1.

    Bilineare Methode

    Die bilineare Methode ist eine Erweiterung der linearen Methode im VI 1D interpolieren. Diese bilineare Methode berechnet die lineare 1D-Interpolation zweimal entlang der x-Achse und gibt die interpolierten Werte bei den Punkten a und b aus. In der folgenden Abbildung ist dies durch die blauen Punkte dargestellt. Anschließend berechnet das VI die lineare 1D-Interpolation entlang der y-Achse (Linienabschnitt, der a und b in der folgenden Abbildung verbindet) und gibt zim, n aus.

    Bikubische Methode

    Führen Sie mithilfe der bikubischen Methode eine Interpolation innerhalb von Gitterrechtecken durch. Diese Methode stellt sicher, dass die inneren interpolierten Oberflächen, deren erste Teilableitungen und die gemischte zweite Ableitung stetig sind.

    Weitere Informationen zur bikubischen Interpolationsmethode finden Sie unter Numerical Recipes in C++ im Hilfethema Literaturhinweise zur Mathematik.

    Bikubische Spline-Methode

    Die bikubische Spline-Methode ist einer Erweiterung der kubischen Spline-Methode im VI "1D interpolieren". Bei dieser Methode wird nacheinander eine Interpolation entlang der beiden Achsen mit Hilfe der kubischen Spline-Methode durchgeführt. Die bikubische Spline-Methode stellt sicher, dass die ersten und zweiten Teilableitungen der Interpolationspolynome stetig sind.

    Weitere Informationen zur bikubischen Spline-Methode finden Sie unter Numerical Recipes in C++ im Hilfethema Literaturhinweise zur Mathematik.

    Beispiele

    Die folgenden Beispieldateien sind in LabVIEW enthalten.

    • labview\examples\Mathematics\Interpolation\2D Interpolation.vi