Dreht eine dreidimensionale kartesische Koordinate anhand des Richtungscosinus entgegen dem Uhrzeigersinn. Zur Auswahl der polymorphen Instanz verbinden Sie Daten mit dem Eingang X oder wählen Sie die Instanz manuell aus.


icon

Ein-/Ausgänge

  • cdbl.png x —

    x ist die reelle x-Komponente am Eingang für einen 2-Element-Vektor.

  • cdbl.png y —

    y ist die reelle y-Komponente am Eingang für einen 2-Element-Vektor.

  • cdbl.png z —

    z gibt die Eingangskoordinate z an.

  • c2ddbl.png Rotationsmatrix —

    Rotationsmatrix gibt die (3,3)-Matrix mit den Richtungscosinuswerten an. Wenn der Rotationsmatrixtyp auf Richtungscosinus eingestellt ist, muss jedes Element der Matrix im Bereich von –1 bis 1 liegen.

  • cu16.png Rotationsmatrixtyp —

    Rotationsmatrixtyp gibt an, ob die Rotationsmatrix die Richtungswinkel oder -cosinuswerte enthält.

    0Richtungswinkel (Standard)—Zeigt an, dass die Rotationsmatrix die Winkel zwischen der x-, y- und z-Achse und die Linien vom Ausgangspunkt der Eingangskoordinaten enthält.
    1Richtungscosinus—Zeigt an, dass die Rotationsmatrix die Cosinuswerte der Richtungswinkel enthält.
  • idbl.png x (Ausgang) —

    x (Ausgang) gibt die gedrehte x-Koordinate aus.

  • idbl.png y (Ausgang) —

    y (Ausgang) gibt die gedrehte y-Koordinate aus.

  • idbl.png z (Ausgang) —

    z (Ausgang) gibt die gedrehte z-Koordinate aus.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Für einen Punkt Psind α, β und γ die Richtungswinkel des Vektors OP, wie in der folgenden Abbildung dargestellt:

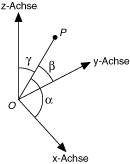
    Der Cosinus des Richtungswinkels wird als Richtungscosinus bezeichnet.

    Vor der Drehung lautet die Koordinate des Punkts P (x, y, z). Nach der Drehung lautet die Koordinate des Punkts P (x', y', z'), wobei

    A ist die Rotationsmatrix, die definiert ist als

    α1,β1undγ1 sind die Richtungswinkel der X'-Achse zu den X-, Y- und Z-Achsen.α2,β2undγ2 sind die Richtungswinkel der Y'-Achse zu den X-, Y- und Z-Achsen.α3,β3undγ3 sind die Richtungswinkel der Z'-Achse zu den X-, Y- und Z-Achsen.