Führt eine diskrete Integration des abgetasteten Signals X durch.


icon

Ein-/Ausgänge

  • c1ddbl.png X —

    X ist das abgetastete Signal zwischen 0 und n –1, wobei n die Anzahl der Elemente in X ist.

  • c1ddbl.png Anfangsbedingung —

    Anfangsbedingung gibt die Anfangsbedingung von X für die Integrationsberechnung an.

    Wenn es sich bei der Integrationsmethode um die Trapezregel oder die Simpson-Regelhandelt, verwendet das VI das erste Element der Anfangsbedingung zur Berechnung der Integration. Wenn es sich bei der Integrationsmethode um die 3/8-Regel von Simpson oder die Bode-Regelhandelt, verwendet das VI die ersten beiden Elemente der Anfangsbedingung zur Berechnung der Integration. Die Standardeinstellung lautet [0].

  • c1ddbl.png Endbedingung —

    Endbedingung gibt die Endbedingung von X für die Integrationsberechnung an.

    Wenn das Integrationsverfahren auf Trapez-Regeleingestellt ist, ignoriert das VI den Parameter Endbedingung. Bei der Integrationsmethode Simpson's Rule oder Simpson's 3/8 Ruleverwendet das VI das erste Element in Final Condition zur Berechnung der Integration. Wenn das Integrationsverfahren auf Bode-Regel eingestellt ist, wird die Integration mit den ersten beiden Elementen in Endbedingung berechnet. Die Standardeinstellung lautet [0].

  • cdbl.png dt —

    dt ist das Sample-Intervall und muss größer als null sein. Der Standardwert lautet 1,0.

    Ist dt kleiner oder gleich 0, ist Integral X ein leeres Array und das VI gibt einen Fehler aus.

  • ci32.png Integrationsverfahren —

    Integrationsverfahren ist das Verfahren, mit dem die Integralrechnung durchgeführt werden soll.

    0Trapez-Regel
    1Simpson-Regel (Standard)
    2Simpsonsche 3/8-Regel
    3Bode-Regel
  • i1ddbl.png Integral X —

    Integral X ist die diskrete Integration von X.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Das Integral x(t) ist definit. Der Wert des Ausgangs-Arrays für einen beliebigen Wert x ist die Fläche unter der Kurve des Eingangs-Arrays zwischen 0 und x.

    Das Integral F(t) der Funktion f(t) ist folgendermaßen definiert:

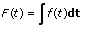
    Gegeben sei y als abgetastete Ausgangsfolge Integral X.

    Wenn das Integrationsverfahren auf Trapez-Regel eingestellt ist, erfasst das VI die Elemente von y mithilfe der folgenden Gleichung:

    für i = 0, 1, 2, …, n – 1,

    wobei n die Anzahl der Samples in X und x–1 der erste Wert in Anfangsbedingung ist.

    Wenn das Integrationsverfahren auf Simpson-Regel eingestellt ist, erfasst das VI die Elemente von y mithilfe der folgenden Gleichung:

    für i = 0, 1, 2, …, n – 1,

    wobei n die Anzahl der Samples in X, x–1 der erste Wert in Anfangsbedingung und xn der erste Wert in Endbedingung ist.

    Wenn das Integrationsverfahren auf Simpsonsche 3/8-Regel eingestellt ist, erfasst das VI die Elemente von y mithilfe der folgenden Gleichung:

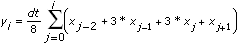
    für i = 0, 1, 2, …, n – 1,

    wobei n die Anzahl der Samples in X ist, x–2 und x–1 das erste und zweite Elemente in Anfangsbedingung sind und xn das erste Element in Endbedingung darstellt.

    Wenn das Integrationsverfahren auf Bode-Regel eingestellt ist, erfasst das VI die Elemente von y mithilfe der folgenden Gleichung:

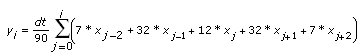
    für i = 0, 1, 2, …, n – 1,

    wobei n die Anzahl der Samples in X ist, x–2 und x–1 das erste und zweite Element in Anfangsbedingung und xn und xn+1 das erste und zweite Element in Endbedingung sind.

    Anfangsbedingung und Endbedingung minimieren den Gesamtfehler durch Erhöhen der Genauigkeit an den Grenzen, besonders bei geringer Anzahl an Samples. Das vorherige Bestimmen der Grenzbedingungen verbessert die Genauigkeit.

    Beispiele

    Die folgenden Beispieldateien sind in LabVIEW enthalten.

    • labview\examples\Mathematics\Probability and Statistics\Probability Density.vi