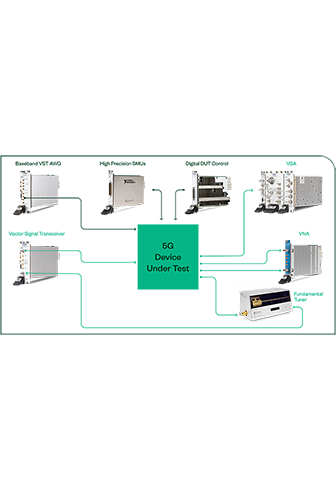
Mit einem NI Partner zusammenarbeiten
Das NI Partner Network ist eine globale Gemeinschaft von Domänen-, Anwendungs- und Testexperten, die mit NI zusammenarbeiten, um Ihre Anforderungen zu erfüllen. NI Partner sind erprobte Anbieter von Produktlösungen, Systemintegratoren, Berater, Produktentwickler sowie Experten für Dienstleistungen und Vertriebskanäle, die über Erfahrungen in einer Vielzahl von Branchen- und Anwendungsbereichen verfügen.