Visualisierung statistischer Daten in LabVIEW
Überblick
Die Visualisierung statistischer Daten bildet einen nützlichen Rahmen, um wertvolle Einblicke in Daten zu gewinnen und die richtige Analysefunktion für die weitere Verarbeitung auszuwählen. Durch diese Art der Darstellung werden Daten sichtbar gemacht, so dass sich Anwender nicht ausschließlich auf abstrakte numerische Werte verlassen müssen. Die Darstellung von Daten wird in der modernen statistischen Analyse immer wichtiger. Ein ganzer Bereich der Statistik, die sogenannte explorative Datenanalyse (EDA), hat sich entwickelt, als Mathematiker herausfanden, dass sie mit dem Computer Daten unter Verwendung grafischer Diagramme schnell darstellen konnten. Werden Muster und Trends hervorgehoben, ermöglichen diese Grafiken das Verständnis der wesentlichen Aussagen von Statistiken auf intuitive Art und Weise.
LabVIEW enthält viele VIs (Virtuelle Instrumente) für unterschiedliche Arten von statistischen Analysen, wie etwa für den arithmetischen Mittelwert und die Standardabweichung. Diese numerischen Statistiken umfassen einfache Berechnungen und bilden damit die Basis der traditionellen statistischen Analyse. Ferner bietet LabVIEW leistungsfähige Hilfsmittel zur grafischen Darstellung, so dass es sich für die EDA sehr gut eignet. Beispielsweise können mit LabVIEW Run Sequence Plots, Streudiagramme, Boxplots, Stem-and-Leaf-Diagramme, Histogramme, Lag Plots, Normal Probability Plots und Quantile-Quantile-Plots erstellt werden. Dieses Dokument enthält Informationen über alle diese Arten der Darstellung.
Im Beispiel-VI „Explorative Datenanalyse“ wird jede der unten besprochenen statistischen Darstellungsmöglichkeiten veranschaulicht. Das Beispiel befindet sich auf dem Datenträger unter <labview>\examples\Mathematics\Probability and Statistics\Exploratory Data Analysis.vi.
Inhalt
- Run Sequence Plots und Streudiagramme
- Boxplots und Stem-and-Leaf-Diagramme
- Histogramme
- Lag Plots
- Normal Probability Plots
- Quantile-Quantile-Plots
Run Sequence Plots und Streudiagramme
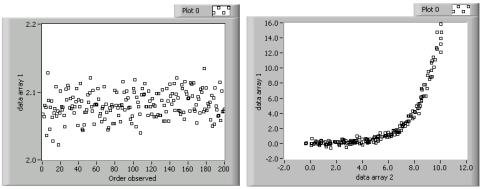
EDA beginnt meist mit einem Run Sequence Plot. Dieses Diagramm stellt Daten in der Reihenfolge dar, in der sie auftreten. Obwohl es recht einfach ist, kann man in diesem Diagramm Ausreißer in den beobachteten Daten erkennen. Ausreißer sind Datenpunkte, die weit vom Mittelwert abweichen und auf einen ernsthaften Messfehler hindeuten können. Bei der Abbildung links handelt es sich um ein Run Sequence Plot. Dieses Diagramm zeigt Daten, die um den Mittelwert streuen. Hier ist kein Ausreißer zu sehen.
Ein Streudiagramm ist eine Verallgemeinerung des Run Sequence Plot. Dieses Diagramm stellt zwei Datensätze gegenüber. Datenpunkte aus jedem Datensatz bilden jeweils ein x/y-Koordinatenpaar, das dann dargestellt wird. In LabVIEW entspricht dieser Prozess der Erstellung eines XY-Grafen. Im Allgemeinen handelt es sich bei den Datensätzen um verschiedene Betrachtungen desselben Ereignisses. So können beispielsweise mit einem Streudiagramm der Treibstoffverbrauch und die Geschwindigkeit eines Fahrzeugs miteinander verglichen werden. Für gewöhnlich werden Datenpunkte mit Bezug auf ihren Beobachtungszeitpunkt gepaart. Die rechte Abbildung oben ist ein Streudiagramm, das die exponenzielle Beziehung zwischen den beiden Datensätzen zeigt. Später kann diese Beziehung mit statistischen Analysen weiter untersucht werden. Das Dokument Run Sequence Plots und Streudiagramme enthält weitere Informationen über die Erstellung solcher Diagramme in LabVIEW.
Boxplots und Stem-and-Leaf-Diagramme
Boxplots zeigen grundlegende zusammengefasste Statistiken eines Datensatzes in Form eines rechteckigen Bildes. Mithilfe von Boxplots kann man Datensätze intuitiv verstehen, denn sie legen weniger Wert auf genaue Datenpunkte und stellen Daten auf eine einzigartige Weise dar. Bei der Abbildung links handelt es sich um einen Boxplot. Das Rechteck steht für den Bereich, in dem sich 50 % der Daten bewegen. Die horizontale Linie in dem Rechteck steht für den Mittelwert des Datensatzes. Die langen vertikalen Linien werden Whiskers genannt. Sie sind 1,5 mal so lang wie ein inneres Quartil, was der Differenz zwischen dem oberen und dem unteren Quartil entspricht. Whiskers werden vom Mittelwert aus gemessen. Sie sind ein indirekter Diagrammindikator, da sie mithilfe anderer statistischer Analysen zustande kommen. Trotzdem sind sie nützlich, denn sie zeigen die Verteilung der Daten sehr deutlich. Ein X steht für einen potenziellen Ausreißer, der sich außerhalb der Reichweite der Whiskers befindet.
Boxplots sind nützlich, da sie schnell den Mittelwert, das obere und untere Quartil sowie potenzielle Ausreißer anzeigen. Werteverteilungen, die nach oben oder unten verschoben sind, haben einen Boxplot, in dem der Mittelwert das Rechteck nicht genau in der Mitte teilt. Zwar schafft ein gleichmäßig unterteilter Boxplot den Eindruck eines normal verteilten Datensatzes, die genauen Einzelwerte des Datensatzes werden jedoch nicht angegeben. Diese Schwäche des Boxplot lässt sich durch ein Stem-and-Leaf Display ("Stamm-Blatt-Diagramm") ausgleichen, das oben rechts abgebildet ist.
Streng genommen sind Stem-and-Leaf Displays keine Diagramme, da sie textbasiert sind. Sie zeigen jedoch jeden Datenpunkt an, so dass auch die genauen Werte bestimmt werden können und nicht nur die Verteilung der Daten. Für Stem-and-Leaf-Diagramme werden die Datensätze in Bereiche, oder auch Stämme, eingeteilt. Jeder Stamm hat eine Reihe von Blättern, also Datenpunkten. Ein Blatt ist die kleinste Nachkommastelle des Stammwertes. In der obigen Abbildung besteht der erste Stamm beispielsweise aus dem Bereich von 2,23 bis 2,27. Dieser Stamm hat drei Blätter: 2,24, 2,26 und 2,27.
Histogramme
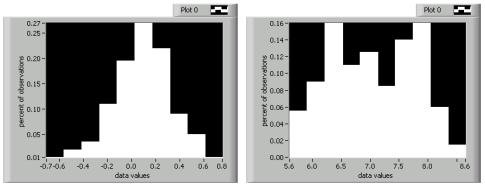
Histogramme ähneln Stem-and-Leaf-Diagrammen, denn jede Anzeige bildet die Anzahl von Datenpunkten ab, die in einem bestimmten Bereich auftreten. Anstatt konkrete Werte zu zeigen, stellt ein Histogramm deren Häufigkeit in Form eines Balkendiagramms dar. In Histogrammen lässt sich die Verteilung der Daten besonders gut erkennen. In folgender Abbildung ist das linke Histogramm ungefähr glockenförmig und das rechte Histogramm hat zwei deutliche Spitzen.
Lag Plots
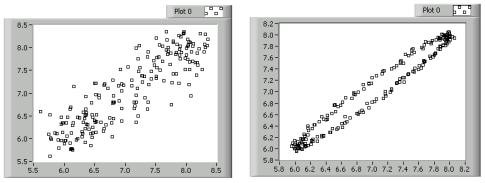
Lag Plots bilden Koordinatenpaare, die sich n Beobachtungen voneinander entfernt befinden. Mit Lag Plots lassen sich zeitverzögerte Beziehungen zwischen Datenpunkten untersuchen. Sie eignen sich zur Analyse von Daten, bei denen zyklische Eigenschaften vermutet werden. So kann ein Lag Plot Datenpunkte einander zuordnen, die sich vier Beobachtungen voneinander entfernt befinden. Lag Plots, die eine lose „Wolke“ von Punkten bilden, weisen nicht auf eine zeitverzögerte Beziehung hin. Formen sie jedoch eine Linie oder eine Ellipse, ist eine starke zeitverzögerte Beziehung vorhanden. Die Lag Plots in folgender Abbildung zeigen zwei zyklische Datensätze.
Normal Probability Plots
Normal Probability Plots vergleichen die Verteilung eines beobachteten Datensatzes mit einem idealen normal verteilten Datensatz. Ein Normal Probability Plot wird erstellt, indem ein idealer Datensatz gebildet wird, der normal verteilte Daten mit derselben Anzahl von Punkten wie der Originaldatensatz beinhaltet. Dann paart man, wie beim Streudiagramm, jeden Punkt des ursprünglichen Datensatzes mit dem entsprechenden Punkt des idealen Datensatzes. Anschließend werden die Paare dargestellt. Folgende Abbildung zeigt zwei Normal Probability Plots.
Quantile-Quantile-Plots
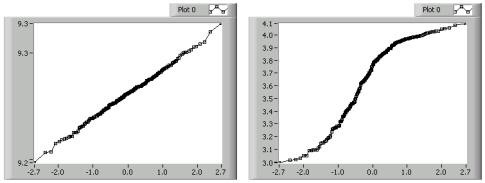
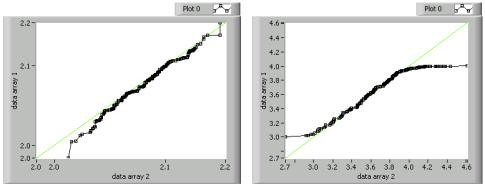
Mit Quantile-Quantile-Plots lässt sich feststellen, ob ein Datensatz stärker verzerrt ist als ein anderer. Diese Plots ähneln Normal Probability Plots. Jedoch wird nicht die Verteilung eines Datensatzes mit einem ideal verteilten Satz verglichen, sondern die Verteilung zweier nach Werten geordneter Datensätze. Liegen Datensätze von ungleicher Größe vor, kann der größere Satz basierend auf dem kleineren Satz interpoliert werden, um die notwendigen Datenpaare bereitzustellen. Folgende Abbildung zeigt zwei Quantile-Quantile-Plots.
Quantile-Quantile-Plots werden genauso interpretiert wie Normal Probability Plots. So deutet ein gerader Plot im 45-Grad-Winkel, wie auf der linken Seite, eine ähnliche Verteilung in beiden Datensätzen an. Der S-förmige Plot rechts deutet darauf hin, dass data array 1 weniger Punkte in den Grenzbereichen hat als data array 2.