Acquiring an Analog Signal: Bandwidth, Nyquist Sampling Theorem, and Aliasing

科學家與工程師經常在實務應用中使用示波器進行類比訊號擷取，並將其轉換為數位訊號以供分析之用。 任何可將類比訊號轉換為數位訊號的裝置，都可稱為示波器。 行動電話就是最常見的一種示波器，它可將擷取到的語音 (類比訊號) 轉換為數位訊號以便傳輸到另一支電話。 不過在測試與量測應用中，示波器 (digitizer) 主要指的是「oscilloscope」(也譯為示波器) 或多功能數位電錶 (DMM)。 本文主要探討的是示波器 (oscilloscope)，但其中大部分主題也可適用於其他種類的示波器 (digitizer)。

無論類型為何，任何一套系統都需要藉助示波器，才能準確地重建波形。 若想要針對不同應用需要選擇適合的示波器 (oscilloscope)，應先了解示波器的運作原理和在購買時考慮該示波器的頻寬、取樣率與解析度。

什麼是頻寬？頻寬 (Bandwidth) 說明了類比前端在最小振幅喪失前提下，將外界訊號傳導至 ADC 的能力，也就是從探針尖端或測試治具傳導到 ADC 輸入。總的來說，示波器前端包含兩大元件：類比輸入路徑與類比轉數位轉換器 (ADC)。 在 ADC 進行數位化之前，類比輸入路徑必須先進行訊號衰減、放大、濾波以及/或是偶合等處理。 然後，ADC 會將處理過的波形取樣，並將類比輸入訊號轉換為可代表類比輸入波形的數位值。 輸入路徑的頻率響應會導致固有的振幅與相位資訊喪失。

圖 1. 頻寬說明了輸入訊號通過示波器前端的兩個頻率範圍部分：類比輸入路徑與 ADC。

可以說，頻寬 (Bandwidth) 主要用以形容一個特定範圍，在這個範圍內，輸入訊號可以用振幅損失最少的方式，穿過類比前端到達 ADC 的輸入端。其說明了示波器可準確量測的頻率範圍。

頻寬的定義為正弦輸入訊號衰減為原始振幅之 70.7% (也可稱為 -3 dB 點) 時的頻率，以赫茲（Hz）為單位。 圖 2 與 3 顯示 100 MHz 示波器的典型輸入響應。

圖 2. 輸入訊號衰減為原始振幅 70.7% 時的頻寬。

圖 3. 本圖表指出在 100 MHz 時，輸入訊號會觸及 -3dB 點。

頻寬的量測範圍，介於訊號振幅降至低於通帶頻率 -3 dB 的頻率點下上限之間。 此種方式看似複雜，但只要拆開來看，實際上相對簡單。

首先計算您的 -3 dB 值。

等式 1. 計算 -3 dB 點

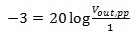
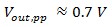
V_in,pp 為輸入訊號的峰值對峰值電壓，而 V_out,pp 則是輸出訊號的峰值對峰值電壓。 例如，當您輸入 1 V 正弦波，輸出電壓可計算為 ，因此 。

由於輸入訊號為正弦波，當輸出訊號觸及此電壓時就會出現兩個頻率；我們稱之為 f₁ 以及 f₂ 角頻率。 這兩種頻率有多種名稱，像是角頻率、截止頻率、交越頻率、半功率頻率、3 dB 頻率與拐點頻率。這些詞彙指的都是相同的數值，而頻寬也是由這兩個數值計算而得。訊號的中央頻率 f₀ 是 f₁ 與 f₂ 的幾何中數。

等式 2. 計算中央頻率

減去兩個角頻率就可計算出頻率 (BW)。

等式 3. 計算頻寬

圖 4. 頻寬、角頻率、中央頻率與 3 dB 點彼此皆有關聯。

計算振幅錯誤

下列是計算頻寬時一種時常派上用場的等式，用於計算振幅錯誤。

等式 4. 計算振幅錯誤

振幅錯誤會以百分比來表示，而 R 則是示波器頻寬與輸入訊號頻率 (f_in) 的比例。

透過以上範例，顯示 100 MHz 示波器具有 100 MHz 正弦波輸入訊號 (1 V 與 BW = 100 MHz，以及 f_in = 100 MHz)， 這表示 R = 1。這時您只需計算等式：

振幅錯誤為 29.3%。 接著，您可以得出 1 V 訊號的輸出電壓：

建議您選擇頻寬高出受量測訊號中相關最高頻率分量的 3 至 5 倍的示波器，以擷取振幅錯誤最小的訊號。 舉例來說，當 1 V 正弦波為 100 MHz，則請使用頻寬介於 300 MHz 至 500 MHz 的示波器。 100 MHz 訊號在這些頻寬的振幅錯誤如下：

計算上升時間 (Rise Time)

輸入訊號的上升時間，指的是訊號最大振幅從 10% 轉至 90% 所需的時間。示波器除了要有合適的頻寬以外，還需同時擁有足夠的上升時間，以準確擷取快速轉變過程中的細節，才能準確量測訊號。在量測脈衝與步進之類的數位訊號時，最需留意這點。某些示波器可能會將此時間訂為 20% 至 80%，請務必參閱您的使用者手冊。

圖 5. 輸入訊號的上升時間，指的是訊號最大振幅從 10% 轉至 90% 所需的時間。

上升時間 (T_r) 計算方式如下：

等式 5. 計算上升時間

常數 k 取決於示波器設定。 大多數頻寬小於 1 GHz 的示波器，其常數值 k 通常為 0.35，而頻寬大於 1 GHz 的示波器，其常數值 K 一般則為介於 0.4 與 0.45。由公式可得：K 值越大，示波器的上升時間越長。

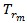
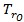
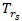
理想的量測上升時間可藉由計算示波器上升時間與輸入訊號的實際上升時間來求得。

等式 6. 計算理想的量測上升時間

建議您將示波器上升時間調整為受量測訊號上升時間的 1/3 至 1/5，以擷取上升時間誤差最小的訊號。

取樣率是了解示波器原理的另一個重要概念。取樣率與頻寬規格並沒有直接關聯。 取樣率是 ADC 將類比輸入波形轉換為數位資料時的頻率。 當類比輸入路徑完成訊號衰減、增益與/或濾波等作業後，示波器會開始對訊號進行取樣，並將最後顯示的波形轉換為數位形式。 整個過程就像是電影中的影格一樣，以快照方式進行。 示波器取樣率越高，波形的解析度會越高，而細節也會越清楚。

奈奎斯特取樣定理 (Nyquist Theorem)

奈奎斯特取樣定理說明了受量測訊號的取樣率與頻率之間的關係。根據此定理，取樣率 f_s 必須比受量測訊號中相關最高頻率分量高出兩倍。 此頻率通常稱為奈奎斯特頻率 f_N。

等式 7. 取樣率必須比奈奎斯特頻率高出兩倍。

為了解其原理，我們將以不同取樣率量測的正弦波為例說明。 在案例 A 中，頻率 f 的正弦波採用相同頻率來取樣。 這些樣本會標示在左側的原始訊號上，而右側建構的訊號則會錯誤顯示為常數 DC 電壓。 在案例 B 中，取樣率為訊號的兩倍。 現在看起來就像是三角波形。 在此情況下，f 等於奈奎斯特頻率，也就是在特定取樣率下用於避免訊號失真的最高頻率分量。 在案例 C 中，取樣率為 4f/3。在此情況下，奈奎斯特頻率為：

因為 f 大於奈奎斯特頻率 (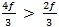)，此取樣率會產生頻率與形狀皆不正確的失真波形。

圖 6. 太低的取樣率會產生不準確的波形重建。

因此，為了準確地重建波形，取樣率 fs 必須比受量測訊號中相關最高頻率分量高出兩倍。 通常我們會讓取樣率比訊號頻率高出五倍左右。

失真

失真發生在訊號擷取過程中，當訊號取樣率小於奈奎斯特頻率的兩倍時，取樣資料中會出現錯誤的較低頻率分量，此現象稱為失真。要避免訊號失真需要特定的取樣率。下圖顯示以 1 MS/s 得出的 800 kHz 正弦波取樣頻率。虛線表示該取樣率下所記錄的失真訊號。 800 kHz 頻率會回到通帶並出現失真現象，同時顯示 200 kHz 正弦波的錯誤頻率。

圖 7. 當取樣率太低，並產生不準確的波形時，就會出現失真情況。

失真頻率 f_a 可在經過計算後，決定超過奈奎斯特頻率的輸入訊號是如何產生的。 此值是樣本頻率最接近的整倍數，減去輸入訊號頻率後的絕對值。

等式 8. 計算失真頻率

例如，假設訊號的取樣頻率為 100 Hz，而輸入訊號內含下列頻率：25 Hz、70 Hz、160 Hz 與 510 Hz。 低於 50 Hz 奈奎斯特頻率的所有頻率皆可正確取樣；超過 50 Hz 的頻率則會失真。

圖 8. 量測不同的頻率值之後，從波形中我們發現其中有些為失真頻率，而其他則為實際頻率。

以下是失真頻率的計算方式：

要防止出現失真情況，除了增加取樣率之外，還可以使用反失真濾波器。 這種低通濾波器可讓任何大於奈奎斯特頻率的輸入訊號頻率衰減，因此必須在 ADC 之前使用，藉此限制輸入訊號頻寬並達到取樣標準。 所有類比輸入通道皆可同時在硬體內實作類比與數位濾波器，以防止失真狀況。

解析度是了解示波器運作原理的另一概念，也是選擇應用所需示波器時的考量要素。解析度位元就是示波器用來呈現訊號的唯一垂直層級數。要了解解析度概念，比較碼尺是一種方式。將碼尺/米尺細分為公釐單位；解析度指的就是碼尺上最小的刻度，也就是 1/1000 單位。

ADC 解析度代表訊號所能分割的最大數量。 振幅解析度受到 ADC 離散輸出層級數量的限制。 二進位碼代表每個分區，因此層級數量計算方式如下：

等式 9. 計算 ADC 離散輸出層級

例如，3 位元示波器具有 2³，也就是 8 個層級。 另一方面，16 位元示波器則具有 2¹⁶，也就是 65,536 個層級。 可偵測的最小電壓變更或編碼寬度計算方式如下：

等式 10. 計算編碼寬度

編碼寬度也稱為最低有效位元 (LSB)。 當裝置輸入範圍介於 0 到 10 V，則 3 位元示波器的編碼寬度為 10/8 = 1.25 V，而 16 位元示波器的編碼寬度為 10/65,536 = 305 μV。 由此可看出，在訊號的顯示方式上差距極大。

圖 9. 解析度介於 16 位元與 3 位元之間的波形差異

一般來說，解析度越高，示波器成本越高；您需要的解析度則需要取決於應用。 請注意，高解析度的示波器不必然代表可提供高準確度； 然而，儀器能達成的準確度卻會受到解析度限制。 解析度會限制量測精確度；解析度 (位元數) 越高，量測精確度就越高。

某些示波器為了讓解析度看起來更高，使用一種稱為「高頻振動」的方法對訊號進行平滑處理。 在處理過程中，高頻振動會刻意將雜訊加進輸入訊號。 這麼做有助於撫平振幅解析度中的細微差異。 其中關鍵在於加入隨機雜訊時，必須讓訊號在連續層級中來回跳動。 這麼做雖能令解析度看起來高，卻也讓訊號雜訊更多。 不過，一旦擷取到訊號後，只要以數位方式取得此雜訊平均值，就能讓訊號平滑化。

圖 10. 高頻振動方式有助於讓訊號平滑化。

• 頻寬、上升時間、取樣率、解析度、失真、奈奎斯特取樣定理 (Nyquist Theorem) 是了解示波器運作原理的重要概念以及挑選示波器時的考量因素。
• 頻寬說明了示波器可準確量測的頻率範圍。 其定義為正弦輸入訊號衰減為原始振幅之 70.7% (也可稱為 -3 dB 點) 時的頻率。
• 頻寬是各個角頻率之間的差異。
• 振幅錯誤為決定系統雜訊時，頻寬與輸入訊號頻率的比例百分比。
• 建議您讓示波器頻寬高出受量測訊號中相關最高頻率分量的 3 至 5 倍，以擷取振幅錯誤最小的訊號。
• 輸入訊號的上升時間，指的是訊號最大振幅從 10% 轉至 90% 所需的時間。
• 建議您將示波器上升時間調整為受量測訊號上升時間的 1/3 至 1/5，以擷取上升時間誤差最小的訊號。
• 取樣率是 ADC 將類比輸入波形轉換為數位資料時的頻率。
• 取樣率至少需為訊號中相關最高頻率的兩倍，不過大多數時候應為五倍左右。
• 失真指的是取樣資料中出現錯誤的頻率分量。
• 解析度位元就是示波器用來呈現訊號的唯一垂直層級數。
• 儀器解析度越高，其精確度就越高。

多功能儀器 - 將桌上型儀器整合為單一固定功能裝置。
了解集混合式訊號示波器、函式產生器、多功能數位電表、可程式化 DC 電源以及數位 I/O 為一體的多合一儀器，以及如何將其搭配您的電腦或 iPad 一起使用，以有效率地進行電路設計、偵測及驗證。

探索專為測試打造的示波器
示波器是許多應用的關鍵，堪稱自動化測試系統的必備儀器。如果您的應用需求包含了資料量測/分析/處理、快速輸出，或是耗電量最低的超小機身，就可以考慮選用模組化解決方案。

若需要完整的線上教學清單，請回到儀器基本概念首頁。