- Document History
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report to a Moderator
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report to a Moderator
Dynamic Tire Load Acquisition for Ground Vehicle Handling Analysis with NI CompactRIO
Contact Information
University and Department: Missouri University of Science and Technology
Team Members: Brandon Doherty
Faculty Advisors: Dr. Hank Pernicka
Primary Email Address:
Primary Telephone Number (include area and country code):
Project Information
Project Title: Dynamic Tire Load Acquisition for Ground Vehicle Handling Analysis with NI CompactRIO
List all parts (hardware, software, etc.) you used to design and complete your project:
CompactRIO Real-time embedded controller with data storage
FPGA Backplane for I/O Modules
8-channel, 24-bit quarter bridge analog input module for strain gauges
Overview
The necessity to understand the real world suspension loads in ground based vehicles has led to the creation of an electronic strain gage instrumentation system. A method developed to dynamically record the normal loads delivered by the tires of an open-wheel racecar was tested on track and discussed. The forces transmitted by each of the vehicle’s four tires were recorded during a series of forward acceleration, braking, and skidpad exercises to determine the highest instantaneous lateral and longitudinal suspension loading. These data were used to verify the calculations and assumptions of a physics-based analytical model that was concerned with the effects of lateral and longitudinal vehicular load transfer under acceleration. -Brandon Doherty (Missouri S&T)
Table of Contents
Introduction
The typical analysis of load transfer from the tires to the chassis of a ground based vehicle often incurs many approximations and assumptions that lead to a high degree of result uncertainty. Concerns including transient longitudinal and lateral load transfers under unpredictable accelerations, non-ideal track surfaces, and unaccounted aerodynamic forces reduce the accuracy of analytical solutions.
In an effort to reduce these uncertainties, actual load data were collected to verify models. This paper outlines a technique to dynamically collect the normal loads from the four wheels of a test vehicle. It is the author’s opinion that the use of strain gages attached to the suspension components of a vehicle can offer results of sufficient accuracy at a reasonable cost.
These force data form the foundation of a vehicle suspension and related support structures design. The accuracy of the calculations and assumptions are of great importance to driver safety as a failure of the suspension or related structures could lead to injury. In addition to avoiding the obvious concerns of component failure, lower load uncertainty can indirectly lead to higher vehicle performance; the required factor of safety for each part can be reduced allowing for less conservative designs with lower mass figures. Designers eager to decrease vehicle mass and increase passenger safety will find value in the load analysis strategy presented in this paper.
See the parts list for this application now!
Experimental Procedure
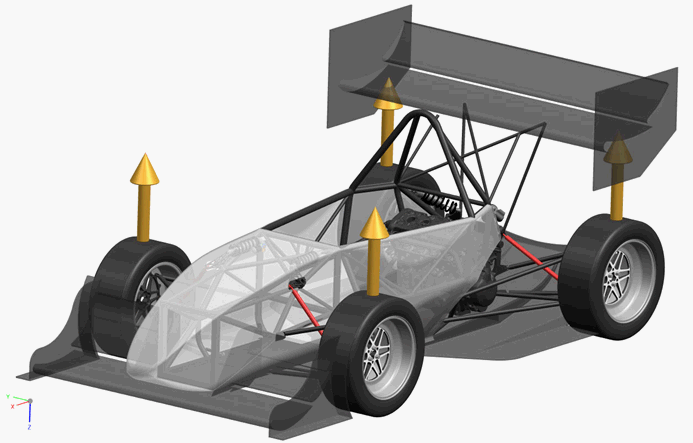
A test vehicle was instrumented to determine the forces within the structures that carry the loads from the tires to the chassis. The car used in this study featured an all-around double wishbone suspension and pushrod activated springs as illustrated in Figure 1. The pushrods, pictured in red, coupled with the springs carry the normal load of the wheels to the chassis as guided by the sweeping motions of the wishbone control arms. This study focuses primarily on the normal loads experienced by the individual wheels. After a brief discussion of system theory, an explanation of how the individual components of the strain gage monitoring system were specified, installed, interpreted, and calibrated is given.
[+] Enlarge Image
Figure 1. Test vehicle with the pushrods highlighted in red and the normal forces highlighted in yellow.
System Theory
To determine the normal load transmitted from the contact patch of the tire to the chassis, an investigation of force induced strain in the pushrod was conducted. The strain present in these structures is proportional to the stress experienced as described by Hooke’s law. No suspension component of any vehicle should surpass its yield strength under normal operating conditions; therefore, the linear relationship described in eq. 1 is reasonable. Rearranging the definition of stress in eq. 2 with eq. 1 leads to the relationship used for strain gage analysis shown in eq. 3.
Eq. 1 Stress = (Modulus of elasticity)*(Strain)
Eq. 2 Stress = (Force)/(Area)
Eq. 3 Force = (Area)*(Modulus of elasticity)*(Strain)
Strain within an axially loaded tube is ideally consistent across its cross-section. This is only true if there are no bending loads present and the tube is loaded along its axis. The pushrods of the test vehicle meet these conditions as they are loaded at their ends with spherical joints. The force transferred by the pushrods can be correlated to measured strain. The relationship of pushrod force and the normal force transferred at the contact patch of each tire is discussed below.
Specification of Components
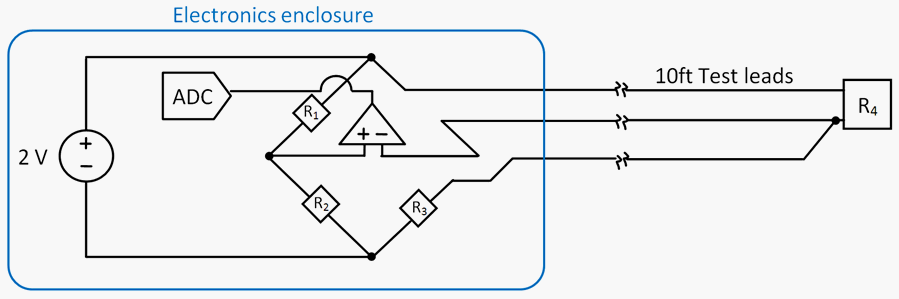
The current state of the art in strain monitoring generally involves electronically measuring the change of resistance in a thin conductor attached to the strained object. The strain gage is usually wired into a Wheatstone bridge to evaluate resistance as a function of voltage. A particular setup called a quarter-bridge was used in all four Wheatstone bridges for its simplicity and low cost. Refer to Figure 2 for layout details.
For the experiment described in this study, 120-ohm Omega SGD-6/120-LY11 strain gages were used to relate strain to resistance. They were chosen for their affordability, ruggedness, and pre-soldered leads. The strain gage is indicated as R4 in Figure 2 while R3, R2, and R1 are precision matched 120-ohm balancing resistors. Twenty-two gage wires were used for all interconnects as recommended by Omega. A third lead was connected to the strain gage to help the bridge balance the effects of wire resistance. A two volt excitation voltage was supplied to all strain gages. Typically a higher voltage is employed, but a precision strain gage amplifier was used to minimize ohmic heating induced error.
The related electronic measurement equipment selection was based on the ability to resolve and record the minute changes in voltage within the Wheatstone bridges at a rate sufficient to capture the fastest expected event. This interpretation is handled by a device known as an analog-to-digital convertor or ADC. Three main requirements were used to select the ADC: number of channels, sampling rate, and resolution.
It was estimated that the fastest the test vehicle could react and settle to driving over a 0.5 inch bump was 0.1 seconds. This bump situation was reasoned to be the quickest event that the instrumentation would be required to capture. To make certain the highest possible instantaneous load was captured and recorded it was decided to sample at a rate of ten times the shortest event time or 100 samples per second. It is required to monitor each pushrod individually as all four wheels experience loads uniquely. The desired overall sample rate was calculated to be 400 samples per second.
The resolution requirement of the device was based on the worst-case load scenario for the front and rear pushrods. It was estimated that the highest expected loads for the front and rear pushrods were 750 and 500 pounds, respectively, during the design phase of the vehicle manufacture. With the expectation that half-pound increments would be sufficient for structural analysis, it was reasoned that the strain gage ADC must have at least a 10 bit resolution (210 steps). Added resolution was deemed desirable as it would allow for greater sensing of transducer overload, a larger load range, and an ability to resolve finer detail in the measured strain.
There are several ADC solutions from different manufactures that satisfactorily meet the project requirements. A National Instruments (NI) arrangement was chosen due to its onsite availability. The project’s instrumentation grade power supply, ADCs, processor, and data logger were all sponsored by NI.
The NI hardware was organized into two components: a CompactRIO Real Time Controller chassis (model NI 9002) and an 8-channel, 24-bit quarter bridge analog input module (model NI 9235). The CompactRio chassis housed the FPGA processor and data memory while the input module contained eight independent ADCs, eight Wheatstone quarter bridges, eight differential amplifiers, and a precision regulated 2-volt excitation power supply. The input module was highly capable. It had the ability to capture 10,000 samples per second per channel and had integrated bridge voltage amplifiers to improve sensitivity. The NI arrangement provided an ideal solution to this instrumentation challenge due to its robust packaging and ease of configuration in the National Instruments LabVIEW software. Figure 3 displays the test equipment used for the experiment.
See the parts list for this application now!

[+] Enlarge Image
Figure 3. Test equipment: CompactRio chassis, instrumented pushrods, and input module with test leads.
Installation of Components
Strain gages require careful installation in order to provide satisfactory results. The pushrods were cleaned of their protective epoxy paint with a wire wheel abrasive tool, roughened with 400-grit sandpaper, scored with parallel alignment marks to ease strain gage installation, and then wiped with mineral spirits to remove any residue debris. One strain gage was affixed to each pushrod of the test vehicle with a thin layer of cyanoacrylate glue. Insulating adhesive tape was placed under the uninsulated leads to prevent shorting once the glue had cured. Three ten-foot wires were then soldered to the uninsulated leads, wrapped around the pushrods, and epoxied in place to provide protection from accidental tugging and road vibration (Figure 4). Next, the bundle of three wires was spliced with weather resistant spade connectors and zip-tied to prevent tangling.
The pushrods were installed into the suspension after calibration. Once the suspension had been aligned, the bundles were connected to the NI input module. The instrumentation chassis was secured under the driver’s legs in the vehicle’s cockpit. A temporary cardboard enclosure was installed during testing to protect the equipment from accidental bumps during driver entry and egress (Figure 5).
Calibrating the Strain Gages
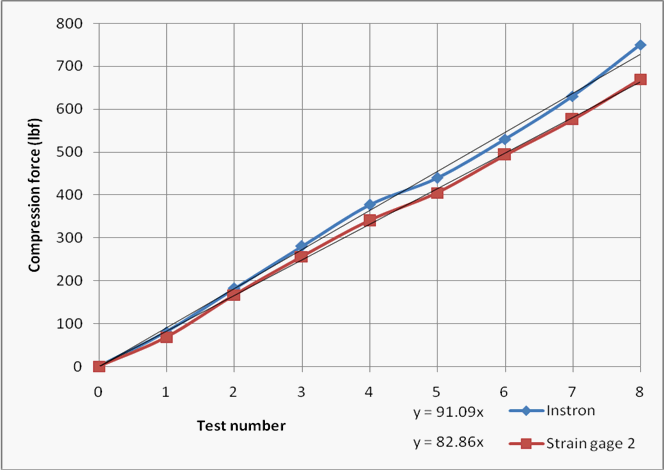
Calibration was performed on each strain gage installation to adjust for uneven test lead resistances, strain gage misalignment, and manufacturing tolerances. The strain gages were evaluated on an Instron tensile testing machine under compression at approximately 100 pound increments up to about 750 pounds (Figure 6). It would have been preferable to calibrate at even increments of exactly 100 pounds, however, the equipment controls did not lend itself to that sort of load-setting precision. The results were graphed and a linear regression was performed to determine the degree of error present in each strain gage (Figure 7).
The strain gages were not perfectly aligned with the axis of the tube during installation and this introduced a systematic linear error. The correction factor could be determined by analyzing the difference in the slopes found in the collected data.
All strain gages consistently measured within five percent of the Instron values over their entire range (0 to 750 pounds) after balancing the resistances in the Wheatstone bridge and accounting for the installation error. Another round of calibration was performed once the pushrods were installed into the test vehicle on four individual scales with similar results.
Interpreting the Strain Gage Readings
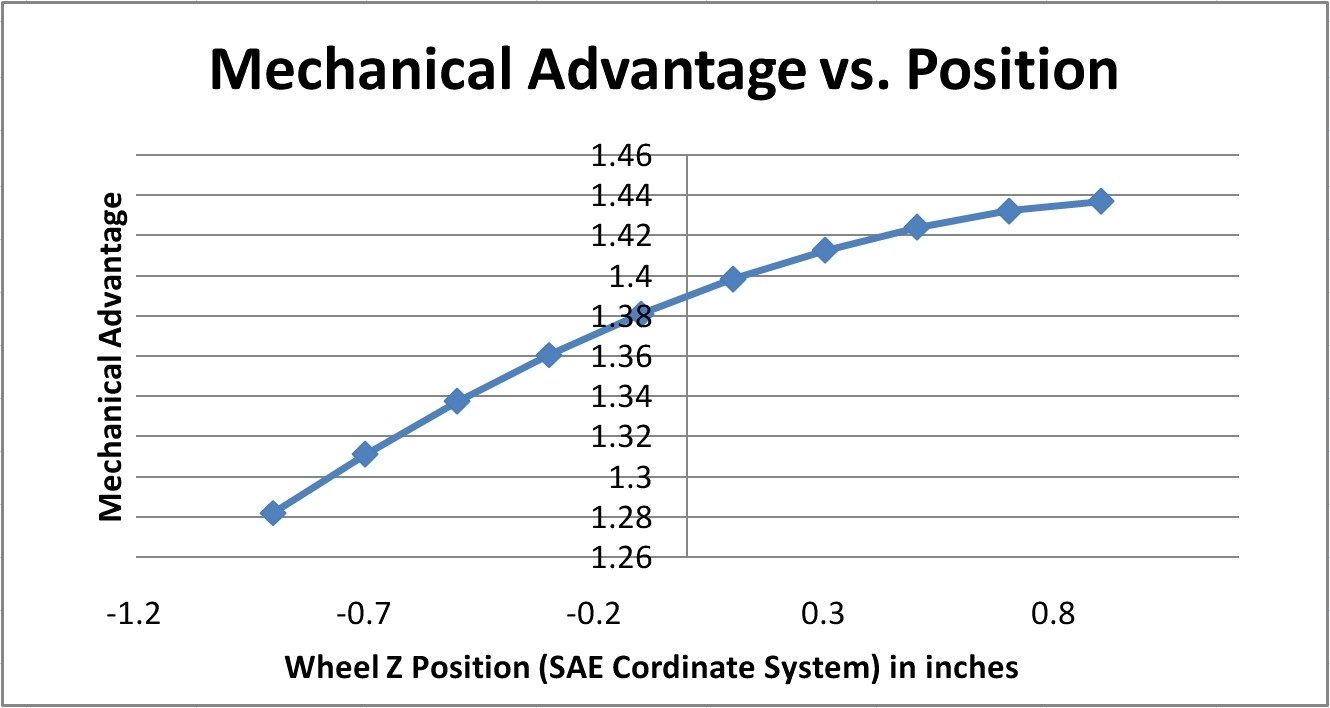
It is important to note that the pushrods carry only the normal load present in the wheels. Also, the actual force carried by the push rods is not linearly related to the normal force experienced by the wheel. This is a result of the sweeping motion caused by the suspension control arms. A nonlinear relationship between wheel movement and pushrod mechanical advantage was observed and this result is imaged in Figure 8.

[+] Enlarge Image
Figure 8. Visualization of mechanical advantage change due to change in ride height in the rear suspension.
A simulation of the suspension motion was performed in SIEMENS NX5 CAD software to understand the effects of this change in mechanical advantage due to wheel position. The results for this investigation are presented in Tables 1 and 2 for the front and rear suspension, respectively. The correlation between position and mechanical advantage was plotted in Graph 2 for the front and Graph 3 for the rear. All lengths were measured in inches.
The mechanical advantage changes a total of 6.0% and 8.4% from static ride height as a result of the sweeping movement of the control arms. For the test described in this study this change in mechanical advantage is considered an uncertainty. At the time of writing this study the wheel position sensors were not installed. In a more sophisticated version of this analysis one could correlate wheel position and mechanical advantage to remove this geometry-caused uncertainty.
It is important to note that the full sample rate of 10,000 samples per channel was recorded. This was done to collect a large number of samples that could be averaged and filtered to produce a more accurate, noise reduced result. The static readings remained steady within ten pounds of the force, including the vibrations and electromagnetic interface generated by the test vehicle’s internal combustion motor. Testing could begin once the correlation between the strain and normal load was developed.
Results and Discussion
A series of tests were run to validate the measurements acquired by the newly instrumented pushrods. The evaluations were meant to introduce the highest possible lateral and longitudinal load transfers into the suspension. The tests included forward acceleration launches, braking, and a clockwise/counter-clockwise skidpad (a circular track).
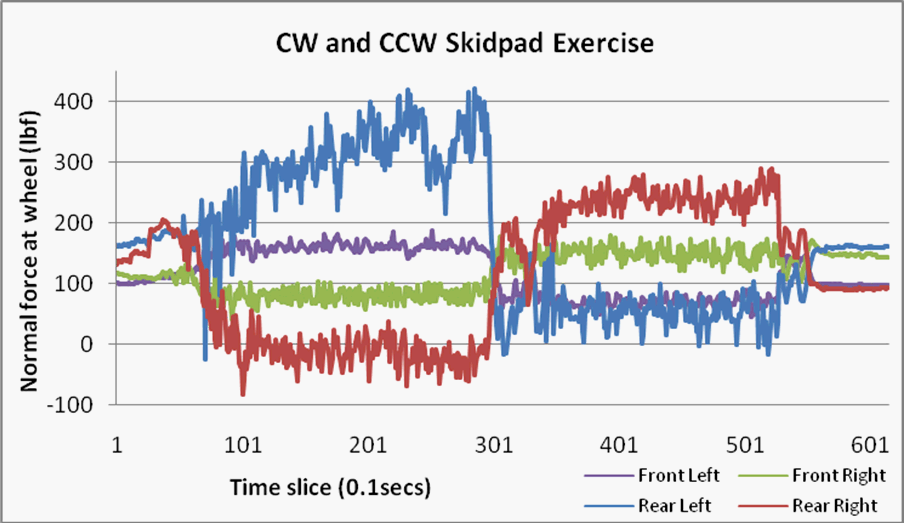
The skidpad was used to generate lateral load transfer. Five laps were completed in the clockwise direction followed by five laps in the counterclockwise direction. Figure 9 shows the processed readings from the skidpad test.
Figure 9 clearly demonstrates the effects of hard corning on lateral load transfer. The data illustrates when the driver entered the skidpad, cornered clockwise, changed direction, and finally exited the track. The effects of centripetal acceleration are clear and the load transfer from left to right can be measured from these results. Approximately 70 percent of the sum sprung vehicle weight transferred laterally during the clockwise laps of the experiment. The driver and the test configured car weighed approximately 575 pounds. It is important to note that the pushrods only sense the weight of the vehicle held by the suspension or sprung weight. The weight of the wheels and suspension knuckles are not carried through the pushrods, but they are transferred directly to the ground. The measured sprung weight of the test configured vehicle with driver was approximately 525 pounds.
It was fascinating and reassuring to note the sum force of all the normal loads remained approximately stable throughout skidpad testing. The skidpad was limited to approximately thirty feet in diameter due to time and resource constraints. The effects of the aerodynamic generated downforce were reduced along with its related increase in grip. This reduction in grip prevented the car from achieving its maximum cornering acceleration and reduced the overall maximum weight transfer. A more stable reading could be obtained with a larger skidpad as it is easier for a driver to maintain a consistent radius with more room allowed for steering correction.
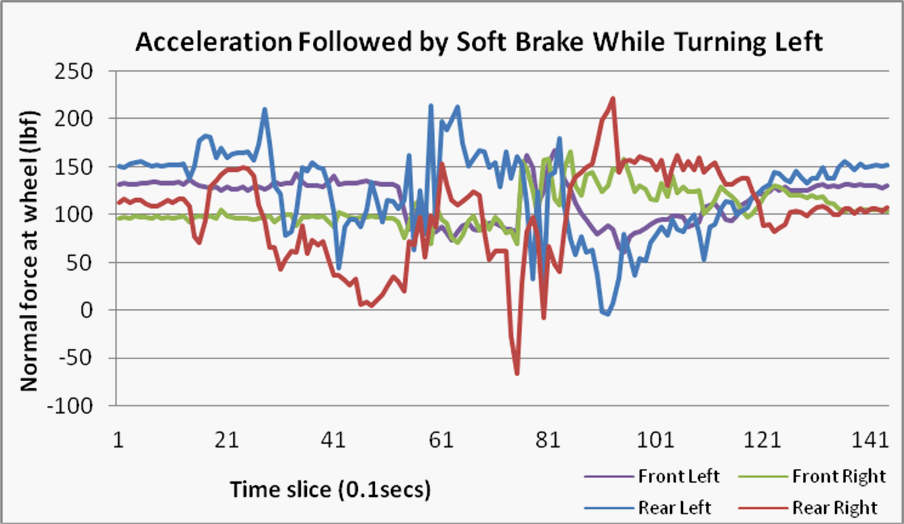
A series of five acceleration launches were run to investigate longitudinal load transfer. Figure 10 displays a capture of one of the launches. At the beginning of the launch (1.1 seconds), the rear of the car witnesses a lower than statically observed weight as the tires begin to rotate. The force in the rear quickly ramped to about 20 percent more than static after the wheels began to develop traction (1.9 seconds). An up gear shift was initiated (2.5 seconds) and the force rebounded to below static, thereafter, climbing again (3.0 seconds) after the second upshift. A final upshift was activated at 3.9 seconds. The brakes were applied (7.5 seconds) and the front of the car finally saw action. The front of the car witnessed an impressive 50 percent increase in normal load at the expense of the rear. In order to position the car for the next acceleration launch the driver began to turn left, but he continued braking (8.5 seconds). During that time an impressive combined lateral and longitudinal weight transfer was observed (9.0 seconds). The sudden transition from straight line acceleration to left cornering slightly pitched the car and this movement loaded the suspension dampers creating an additional normal force on the right wheels.
A final test involving repeated heavy braking was conducted to analyze the effects of longitudinal load transfer. Figure 11 illustrates the results of four consecutive braking exercises. The braking test track was setup as a long ellipse to allow for the highest possible speed before braking. A more ideal track involving two long straight-aways would have been preferred; however, a parking lot of satisfactory size was not available for testing.
The test driver completed four laps on the track and his consistency is visible in the data. The front of the car consistently showed a 50 percent loading increase under heavy braking while the rear loading repeatedly dropped to zero. Negative values are not unreasonable as the pushrods should experience tension when lifting the unsprung weight of the wheels, however, the negative values of over 50 pounds are suspicious and will be subject to further investigation. It is possible the sudden loading of the dampers in fast motion rebound are responsible for the unexpectedly low negative values.
When braking the car generally lurched forward on its suspension while slightly lifting the rear. This was usually followed by the rear abruptly returning to level. The transient peaks between 250 and 300 pounds witnessed in the rear left pushrod are attributed to damper loading caused by rapid shock movement.
The instrumented test vehicle witnessed an approximately 70 percent load transfer under sustained cornering and an approximately 50 percent longitudinal load transfer during heavy braking. During forward acceleration an ~20 percent increase of normal load was measured in the rear wheels while no significant change was observed in the front. Further testing with the strain gauge instrumented vehicle in warm weather and proper sized track will reveal the true maximum normal loads and weight transfer figures.
Conclusion and Recommendations
The experimental strain gage based apparatus successfully captured the normal forces present in the four wheels of the test vehicle. The effects of heavy lateral and longitudinal acceleration were related to their respective load transfers. The results collected within this study along with future track testing will be of great value in refining future test vehicles.
Though the results are of a satisfactory quality to aid future structural design, further efforts could increase the precision of the testing apparatus. For example, it was noted that flexing the wire bundles could introduce a measurable ripple of several pounds into the collected data. The wire resistance changed as the cross-sectional area deformed during bending. This effect could be reduced by choosing thicker leads with stiffer insulation. Also, proper shielding and a reduction in wire length should also improve signal quality. The usefulness of extracted data is directly related to the consistency of the test track. Pavement quality, changes in track elevation, and ambient temperature affect tire force generating performance. Logging strain gage data continuously during the lifetime of the vehicle or testing on a professionally maintained track in a warm, sunny location could experimentally determine the absolute maximum normal forces and load transfer figures.
Acknowledgements
The author would like to thank Eric Cunningham of National Instruments for his assistance in facilitating the delivery of the primary test equipment. To David Erdos, whose LabVIEW knowledge proved invaluable to completing the project within schedule. To my fellow S&T Racing teammates for their cooperation and effort. And many thanks are in order to Dr. Hank Pernicka of the Mechanical and Aerospace Engineering Department of the Missouri University of Science and Technology for his incredible patience and encouragement.