Introduction to 802.11ax High-Efficiency Wireless
Overview
802.11ax, also called High-Efficiency Wireless (HEW), has the challenging goal of improving the average throughput per user by a factor of at least 4X in dense user environments. This new standard focuses on implementing mechanisms to serve more users a consistent and reliable stream of data (average throughput) in the presence of many other users. This paper will explore the new mechanisms that will give the popular 802.11ax standard the title of High-Efficiency Wireless.
Contents
- Introduction
- Key Features and Applications
- Current Challenges to Wi-Fi Throughput in Dense Environments
- PHY Mechanisms for High Efficiency
- MAC Mechanisms for High Efficiency
- 802.11ax Test Challenges
- Conclusion
- About NI and the 802.11ax standard
- References
Introduction
In 2015 the iconic car manufacturer, Ferrari, released a new version of its entry-level model: the Ferrari California T. This sleek sports car has a 3.9 liter turbocharged V8 engine capable of generating more than 412 KW (553 Horsepower), good for smashing zero to 100 Km/h (0 to 62 mph) in 3.6 seconds. Keeping the foot on the accelerator will propel this engineering marvel to its top speed of 315 Km/h (196 mph). [1]
The Ferrari designers considered many details of the engine, body and interior to make this vehicle a daily driver, while delivering the most precise handling, fluid motion, and performance at breakneck speeds. That kind of design would certainly make for an exhilarating – though significantly shorter – daily commute to the office. However, what good would that red Ferrari convertible be on the heavily congested streets of a large metropolitan area, with mostly stop-and-go traffic?
Today many people find themselves in that kind of situation. Perhaps not as privileged to be driving an Italian sports car, but able to enjoy blazing fast wireless connectivity links. Consider that the first 802.11b Wi-Fi standard (1999), had a top link speed of 11 Mbps. A good first step, but significantly slower than a wired connection. Then a few years later the 802.11a/g revision (2003) increased the speed to 54 Mbps with the introduction of Orthogonal Frequency Division Multiplexing (OFDM) technology.
The next link speed improvement came with 802.11n (2009) presenting users with single stream links up to 150 Mbps. The 802.11ac revision of the standard (2013) brought with it the possibility of link speeds around 866 Mbps on a single spatial stream with wider channels (160MHz) and higher modulation orders (256-QAM). Using the specified maximum number of 8 spatial streams, this engineering marvel would, in theory, reach its top speed of 6.97 Gbps. In theory, using 802.11ac is the equivalent of replacing your bicycle or even your family sedan with a souped-up Ferrari.
However, speeds approaching 7 Gbps might only be achievable in the controlled race-track environment of the RF lab. In reality, users commonly experience frustratingly slow data traffic when trying to check their email on a public Wi-Fi at a busy airport terminal. A new revision of the IEEE 802.11 wireless LAN standard – 802.11ax – seeks to remedy exactly this precise situation.
802.11ax, also called High-Efficiency Wireless (HEW), has the challenging goal of improving the average throughput per user by a factor of at least 4X in dense user environments. Looking beyond the raw link speeds of 802.11ac, this new standard implements several mechanisms to serve more users consistent and reliable data throughput in crowded wireless environments.
Key Features and Applications
High-Efficiency Wireless includes the following key features:
- Backwards compatible with 802.11a/b/g/n/ac
- Increase 4X the average throughput per user in high-density scenarios, such as train stations, airports and stadiums.
- Data rates and channel widths similar to 802.11ac, with the exception of new Modulation and Coding Sets (MCS 10 and 11) with 1024-QAM.
- Specified for downlink and uplink multi-user operation by means of MU-MIMO and Orthogonal Frequency Division Multiple Access (OFDMA) technology.
- Larger OFDM FFT sizes (4x larger), narrower subcarrier spacing (4X closer), and longer symbol time (4X) for improved robustness and performance in multipath fading environments and outdoors.
- Improved traffic flow and channel access
- Better power management for longer battery life
High-Efficiency Wireless also serves the following target applications:
- Cellular data offloading: By 2020, 38.1 exabytes Wi-Fi offload traffic will be generated each month, continuing to exceed projected monthly mobile/cellular traffic (30.6 exabytes). [2] That’s equivalent to moving more than 6000 Blue-ray movies per minute on these networks.
- Environments with many access points and a high-concentration of users with heterogeneous devices (Airport Wi-Fi ≠ Home Wi-Fi)
- Outoors/outdoors mixed environments.
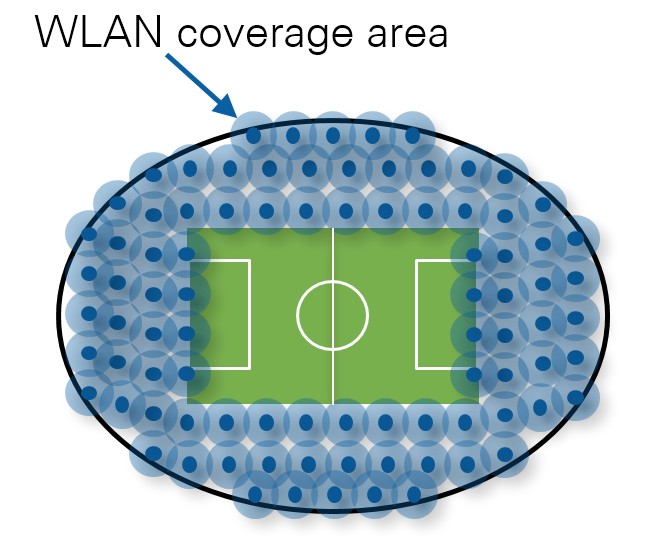
Figure 1. Example scenario of a stadium with high user density and mixed environments targeted for 802.11ax deployment
Current Challenges to Wi-Fi Throughput in Dense Environments
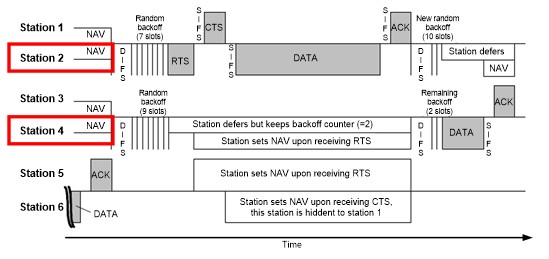
The 802.11 protocol uses a carrier sense multiple access (CSMA) method in which the wireless stations (STA) first sense the channel and attempt to avoid collisions by transmitting only when they sense the channel to be idle. That is, when they don’t detect any 802.11 signals. When an STA hears another one, it waits for a random amount of time for that STA to stop transmitting before listening again for the channel to be free. When they’re able to transmit, STAs transmit their whole packet data.
Wi-Fi STAs may use Request to Send/Clear to Send (RTS/CTS) to mediate access to the shared medium. The Access Point (AP) only issues a CTS packet to one STA at a time, which in turn sends its entire frame to the AP. The STA then waits for an acknowledgement packet (ACK) from the AP indicating that it received the packet correctly. If the STA doesn’t get the ACK in time, it assumes the packet collided with some other transmission, moving the STA into a period of binary exponential backoff. It will try to access the medium and re-transmit its packet after the backoff counter expires.
Figure 2. Clear Channel Assessment Protocol
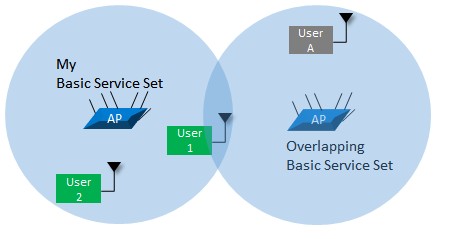
Although this Clear Channel Assessment and Collision Avoidance protocol serves well to divide the channel somewhat equally among all participants within the collision domain, its efficiency decreases when the number of participants grows very large. Another factor that contributes to network inefficiency is having many APs with overlapping areas of service. Figure 3 depicts a user (User 1) that belongs to the Basic Service Set (BSS, a set of wireless clients associated to an AP) on the left. User 1 would contend for access to the medium with other users in its own BSS and then exchange data with its AP. However, this user would still be able to hear traffic from the overlapping BSS on the right.
Figure 3. Medium access inefficiency from overlapping BSS
In this case, traffic from the OBSS would trigger User 1’s backoff procedure. This kind of situation results in users having to wait longer for their turn to transmit, effectively lowering their average data throughput.
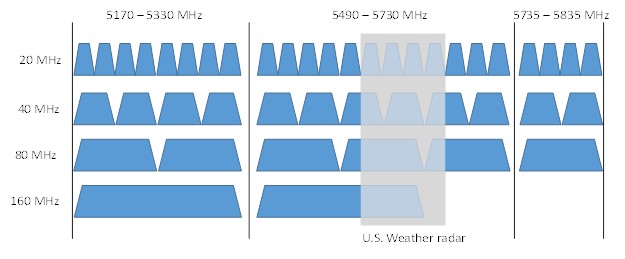
A third factor to consider is the shared use of wider channels. For example, for 802.11ac operation in North America there is only one 160 MHz channel available, and in Europe only two.
Figure 4. Example 802.11ax channel allocation on the 5GHz band
Planning dense coverage with a reduced number of channels becomes very difficult, forcing network managers to reuse channels in nearby cells. Without careful and deliberate power management, users will experience co-channel interference, which degrades performance and negates much of the expected gain from the wider channels. This is especially true for the top data rates of MCS 8, 9, 10, and 11, which are much more susceptible to low signal to noise ratio. Also, on the current implementation of 802.11 networks a 20 MHz channel overlapping an 80 MHz channel will basically render the 80 MHz channel useless, while a user transmits on the narrower channel. Implementing 802.11ac’s Channel Sharing in a high density network compromises the gains of the 80 MHz channel for transmissions on a 20 MHz channel.
PHY Mechanisms for High Efficiency
PHY Changes
The 802.11ax specification introduces significant changes to the physical layer of the standard. However, it maintains backward compatibility with 802.11a/b/g/n and /ac devices, such that an 802.11ax STA can send and receive data to legacy STAs. These legacy clients will also be able to demodulate and decode 802.11ax packet headers – though not whole 802.11ax packets – and backoff when an 802.11ax STA is transmitting.
The following table highlights the most important changes to this revision of the standard, in contrast to the current 802.11ac implementation:
802.11ac | 802.11ax | |
BANDS | 5 GHz | 2.4 GHz and 5 GHz |
CHANNEL BANDWIDTH | 20 MHz, 40 MHz, 80 MHz, 80+80 MHz & 160 MHz | 20 MHz, 40 MHz, 80 MHz, 80+80 MHz & 160 MHz |
FFT SIZES | 64, 128, 256, 512 | 256, 512, 1024, 2048 |
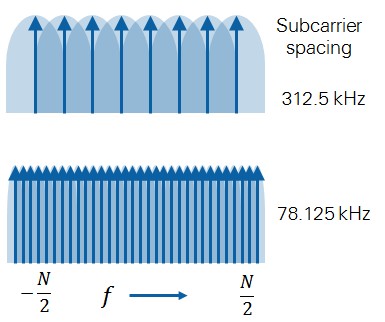
SUBCARRIER SPACING | 312.5 kHz | 78.125 kHz |
OFDM SYMBOL DURATION | 3.2 us + 0.8/0.4 us CP | 12.8 us + 0.8/1.6/3.2 us CP |
HIGHEST MODULATION | 256-QAM | 1024-QAM |
DATA RATES | 433 Mbps (80 MHz, 1 SS) 6933 Mbps (160 MHz, 8 SS) | 600.4 Mbps (80 MHz, 1 SS) 9607.8 Mbps (160 MHz, 8 SS) |
Table 1. 802.11ac vs. 802.11ax
Notice that the 802.11ax standard will operate in both the 2.4 GHz and 5 GHz bands. The specification defines a four times larger FFT, multiplying the number of subcarriers. However, one critical change with 802.11ax is that the subcarrier spacing has been reduced to one fourth the subcarriers spacing of previous 802.11 revisions, preserving the existing channel bandwidths.
Figure 5. Narrower sub-carrier spacing
The OFDM symbol duration and cyclic prefix also increased 4X, keeping the raw link data rate the same as 802.11ac, but improving efficiency and robustness in indoor/outdoor and mixed environments. Nevertheless, the standard does specify 1024-QAM and smaller cyclic prefix ratios for indoor environment, which will increase the maximum data rate.
Beamforming
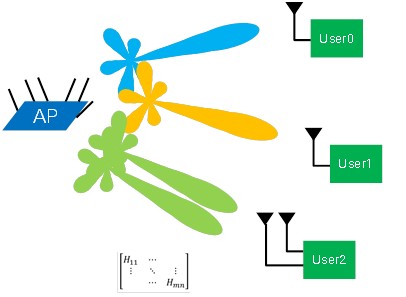
802.11ax will employ an explicit beamforming procedure, similar to that of 802.11ac. Under this procedure, the beamformer initiates a channel sounding procedure with a Null Data Packet. The beamformee measures the channel and responds with a beamforming feedback frame, containing a compressed feedback matrix. The beamformer uses this information to compute the channel matrix, H. The beamformer can then use this channel matrix to focus the RF energy toward each user.
Multi-User Operation: MU-MIMO and OFDMA
The 802.11ax standard has two modes of operation:
Single User: in this sequential mode the wireless STAs send and receive data one at a time once they secure access to the medium, as this paper has described above.
Multi-User: this mode allows for simultaneous operation of multiple non-AP STAs. The standard divides this mode further into Downlink and Uplink Multi-user.
- Downlink multi-user refers to data that the AP serves to multiple associated wireless STAs at the same time. The existing 802.11ac standard already specifies this feature.
- Uplink multi-user involves simultaneous transmission of data from multiple STAs to the AP. This is new functionality of the 802.11ax standard, which did not exist in any of the previous versions of the Wi-Fi standard.
Under the Multi-User mode of operation, the standard also specifies two different ways of multiplexing more users within a certain area: Multi-User MIMO and Orthogonal Frequency Division Multiple Access (OFDMA). For both of these methods, the AP acts as the central controller of all aspects of multi-user operation, similar to how an LTE cellular base station controls the multiplexing of many users. An 802.11ax AP can also combine MU-MIMO with OFDMA operation.
Multi-User MIMO
Borrowing from the 802.11ac implementation, 802.11ax devices will use beamforming techniques to direct packets simultaneously to spatially diverse users. That is, the AP will calculate a channel matrix for each user and steer simultaneous beams to different users, each beam containing specific packets for its target user. 802.11ax supports sending up to eight multi-user MIMO transmissions at a time, up from four for 802.11ac. Also, each MU-MIMO transmission may have its own Modulation and Coding Set (MCS) and a different number of spatial streams. By way of analogy, when using MU-MIMO spatial multiplexing, the AP could be compared to an Ethernet switch that reduces the collision domain from a large computer network to a single port.
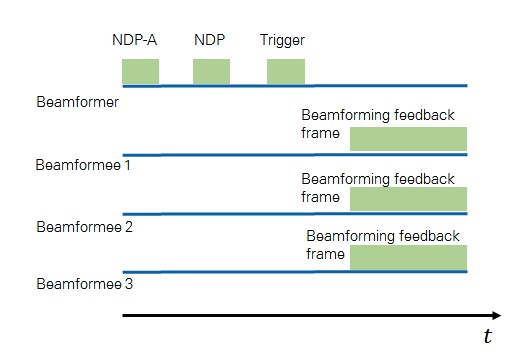
As a new feature in the MU-MIMO Uplink direction, the AP will initiate a simultaneous uplink transmission from each of the STAs by means of a trigger frame. When the multiple users respond in unison with their own packets, the AP applies the channel matrix to the received beams and separates the information that each uplink beam contains. The AP may also initiate Uplink multi-user transmissions to receive beamforming feedback information from all participating STAs as shown in Figure 7.
Figure 6. AP using MU-MIMO beamforming to serve multiple users located in spatially diverse positions
Figure 7. A beamformer (AP) requesting channel information for MU-MIMO operation
Multi-User OFDMA
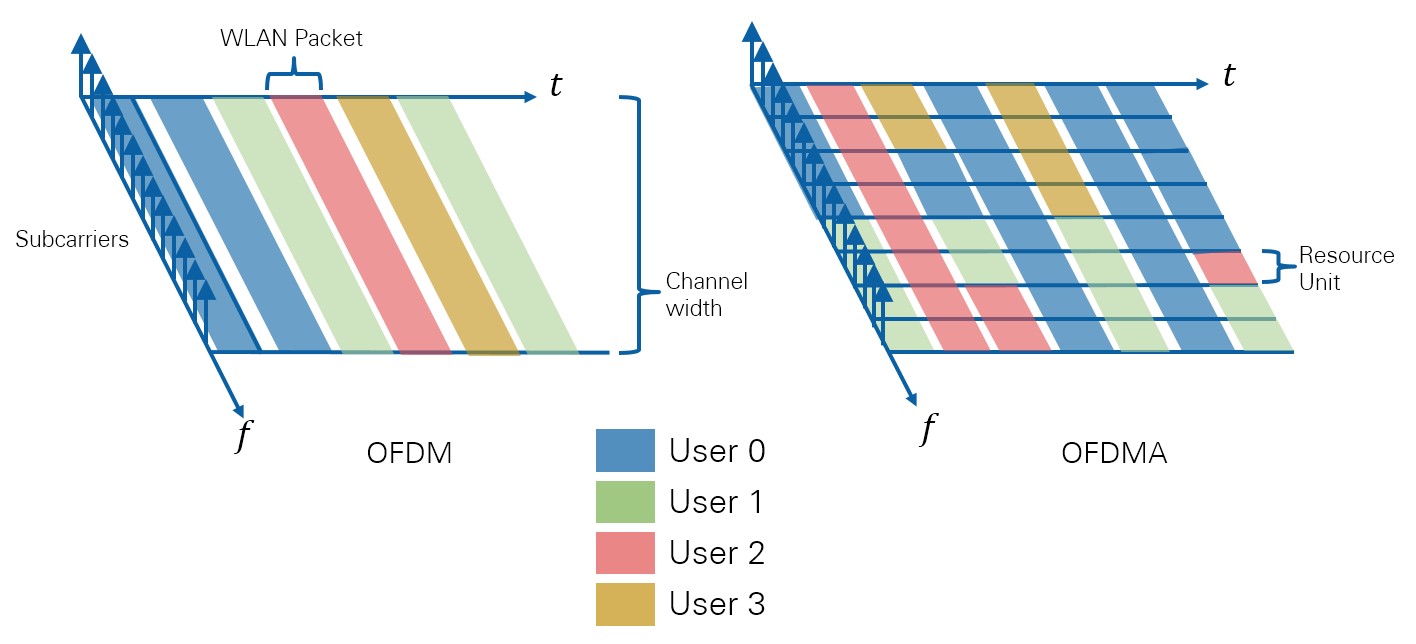
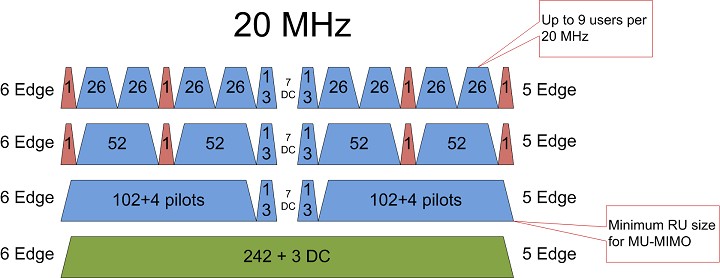
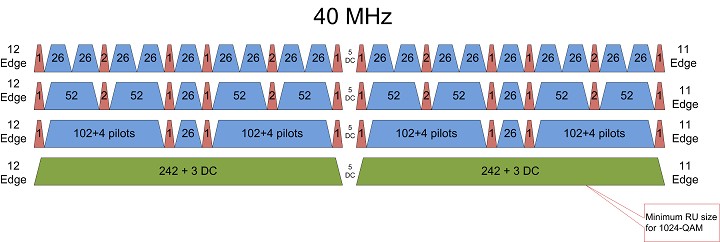
The 802.11ax standard borrows a technological improvement from 4G cellular technology to multiplex more users in the same channel bandwidth: Orthogonal Frequency-Division Multiple Access (OFDMA). Building on the existing orthogonal frequency-division multiplexing (OFDM) digital modulation scheme that 802.11ac already uses, the 802.11ax standard further assigns specific sets of subcarriers to individual users. That is, it divides the existing 802.11 channels (20, 40, 80 and 160 MHz wide) into smaller sub-channels with a predefined number of subcarriers. Also borrowing from modern LTE terminology, the 802.11ax standard calls the smallest subchannel a Resource Unit (RU), with a minimum size of 26 subcarriers.
Based on multi-user traffic needs, the AP decides how to allocate the channel, always assigning all available RUs on the downlink. It may allocate the whole channel to only one user at a time – just as 802.11ac currently does – or it may partition it to serve multiple users simultaneously (see Figure 8).
Figure 8. A single user using the channel Vs. multiplexing various users in the same channel using OFDMA
In dense user environments where many users would normally contend inefficiently for their turn to use the channel, this OFDMA mechanism now serves them simultaneously with a smaller – but dedicated – subchannel, thus improving the average throughput per user. Figure 9illustrates how an 802.11ax system may multiplex the channel using different RU sizes. Note that the smallest division of the channel accommodates up to 9 users for every 20MHz of bandwidth. [4]
Figure 9. Subdividing Wi-Fi channels using various Resource Unit sizes
The following table shows the number of users that can now get frequency-multiplexed access when the 802.11ax AP and STAs coordinate for MU-OFDMA operation.
RU type | CBW20 | CBW40 | CBW80 | CBW160 and CBW80+80 |
26-subcarrier RU | 9 | 18 | 37 | 74 |
52-subcarrier RU | 4 | 8 | 16 | 32 |
106-subcarrier RU | 2 | 4 | 8 | 16 |
242-subcarrier RU | 1-SU/MU-MIMO | 2 | 4 | 8 |
484-subcarrier RU | N/A | 1-SU/MU-MIMO | 2 | 4 |
996-subcarrier RU | N/A | N/A | 1-SU/MU-MIMO | 2 |
2x996 subcarrier RU | N/A | N/A | N/A | 1-SU/MU-MIMO |
Table 2. Total number of RUs by channel bandwidth
Multi-User Uplink Operation
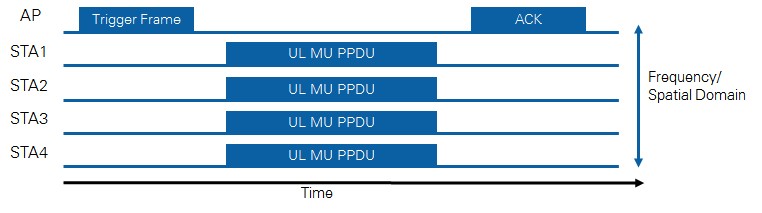
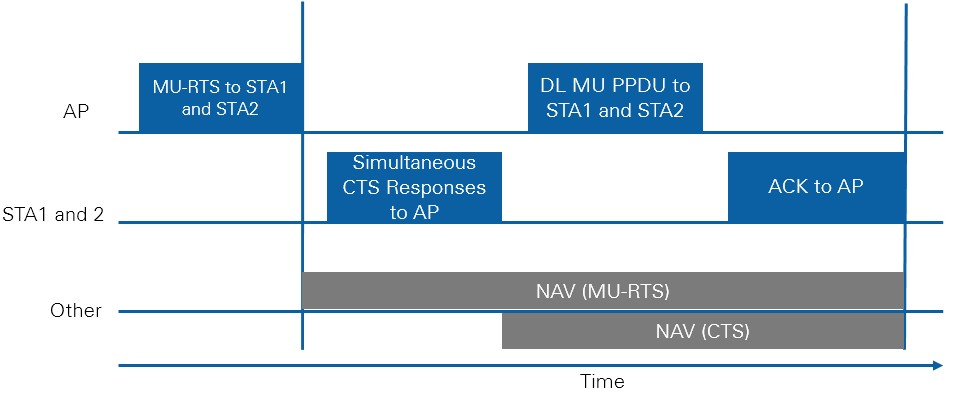
To coordinate uplink MU-MIMO or uplink OFDMA transmissions the AP sends a trigger frame to all users. This frame indicates the number of spatial streams and/or the OFDMA allocations (frequency and RU sizes) of each user. It also contains power control information, such that individual users can increase or reduce their transmitted power, in an effort to equalize the power that the AP receives from all uplink users and improve reception of frames from nodes farther away. The AP also instructs all users when to start and stop transmitting. As Figure 10depicts, the AP sends a multi-user uplink trigger frame that indicates to all users the exact moment at which they all start transmitting, and the exact duration of their frame, to ensure that they all finish transmitting simultaneously as well. Once the AP receives the frames from all users, it sends them back a block ACK to finish the operation.
Figure 10. Coordinating uplink multi-user operation
One of the main goals of the 802.11ax is to support 4X higher average per-user throughput in dense user environments. With that goal in mind, the standard designers have specified that 802.11ax devices support Downlink and Uplink MU-MIMO operation, MU-OFDMA operation, or both for an even larger number of simultaneous users.
MAC Mechanisms for High Efficiency
Spatial Reuse with Color Codes
To improve the system level performance and the efficient use of spectrum resources in dense deployment scenarios, the 802.11ax standard implements a spatial reuse technique. STAs can identify signals from overlapping Basic Service Sets (BSS) and make decisions on medium contention and interference management based on this information.
When an STA that is actively listening to the medium detects an 802.11ax frame, it checks the BSS color bit or MAC address in the MAC header. If the BSS color in the detected PPDU is the same color as the one that its associated AP has already announced, then the STA considers that frame as an intra-BSS frame.
However, if the detected frame has a different BSS color than its own, then the STA considers that frame as an inter-BSS frame from an overlapping BSS. The STA then treats the medium as BUSY only during the time it takes the STA to validate that the frame is from an inter-BSS, but not longer than the time indicated as the length of the frame’s payload.
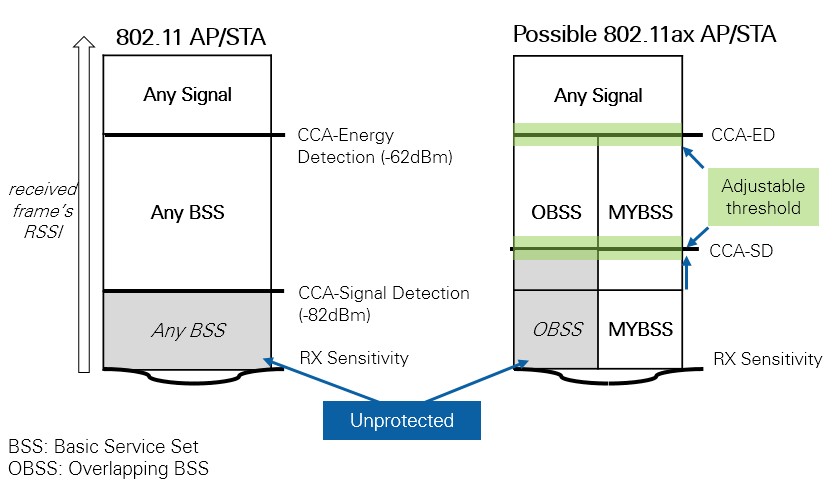
The standard still has to define some of the mechanisms for ignoring traffic from overlapping BSSs, but the implementation could include raising the clear channel assessment signal detection (SD) threshold for inter-BSS frames, while maintaining a lower threshold for intra-BSS traffic (see Figure 11). That way, traffic from neighboring BSS wouldn’t create unnecessary channel access contention.
Figure 11. Using Color Codes for Clear Channel Assessment
When 802.11ax STAs use the color code based CCA rule, they are also allowed to adjust the OBSS signal detection threshold together with transmit power control. This adjustment improves system level performance and the use of spectrum resources. Furthermore, 802.11ax STAs can adjust CCA parameters, such as the energy detection level and the signal detection level.
In addition to using CCA to determine if the medium is idle or busy for the current frame, the 802.11 standard employs a Network Allocation Vector (NAV) – a timer mechanism that maintains a prediction of future traffic – for STAs to indicate the time required for the frames immediately following the current frame. The NAV acts as a virtual carrier sense that ensures medium reservation for frames critical to operation of the 802.11 protocol, such as control frames, and data and ACKs following an RTS/CTS exchange.
Figure 12. Example of MU PPDU exchange and NAV setting
The 802.11 Task Group working on High-Efficiency Wireless will possibly include not just one NAV field, but two different NAVs to the 802.11ax standard. Having an intra-BSS NAV and an inter-BSS NAV could help STAs to predict traffic within their own BSS and feel free to transmit when they know the state of overlapping traffic.
Power-saving with Target Wake Time
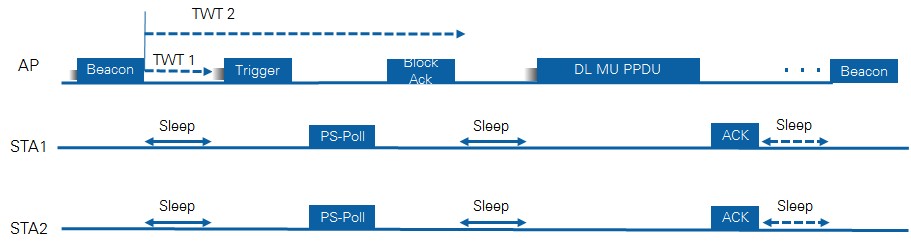
An 802.11ax AP can negotiate with the participating STAs the use of the Target Wake Time (TWT) function to define a specific time or set of times for individual stations to access the medium. The STAs and the AP exchange information that includes an expected activity duration. This way the AP controls the level of contention and overlap among STAs needing access to the medium. 802.11ax STAs may use TWT to reduce energy consumption, entering a sleep state until their TWT arrives. Furthermore, an AP can additionally devise schedules and deliver TWT values to STAs without individual TWT agreements between them. The standard calls this procedure Broadcast TWT operation (see Figure 13).
Figure 13. Example of Target Wake Time Broadcast operation
802.11ax Test Challenges
Tighter EVM requirement
The 802.11ax standard now mandates support for 1024-QAM. Additionally, the subcarriers are only 78.125 KHz away from each other. This means that 802.11ax devices need to have oscillators with improved phase noise performance and RF front ends with better linearity. The test instruments that measure DUT behavior in turn require their EVM noise floor to be significantly lower than the DUT’s.
The following table lists the EVM levels that 802.11ax-compliant devices will likely have to meet.
| 16-QAM | 64-QAM | 256-QAM | 1024-QAM |
802.11ax EVM requirement | -19 dB | -27 dB | -32 dB | -35 dB |
Table 3. 802.11ax EVM requirements
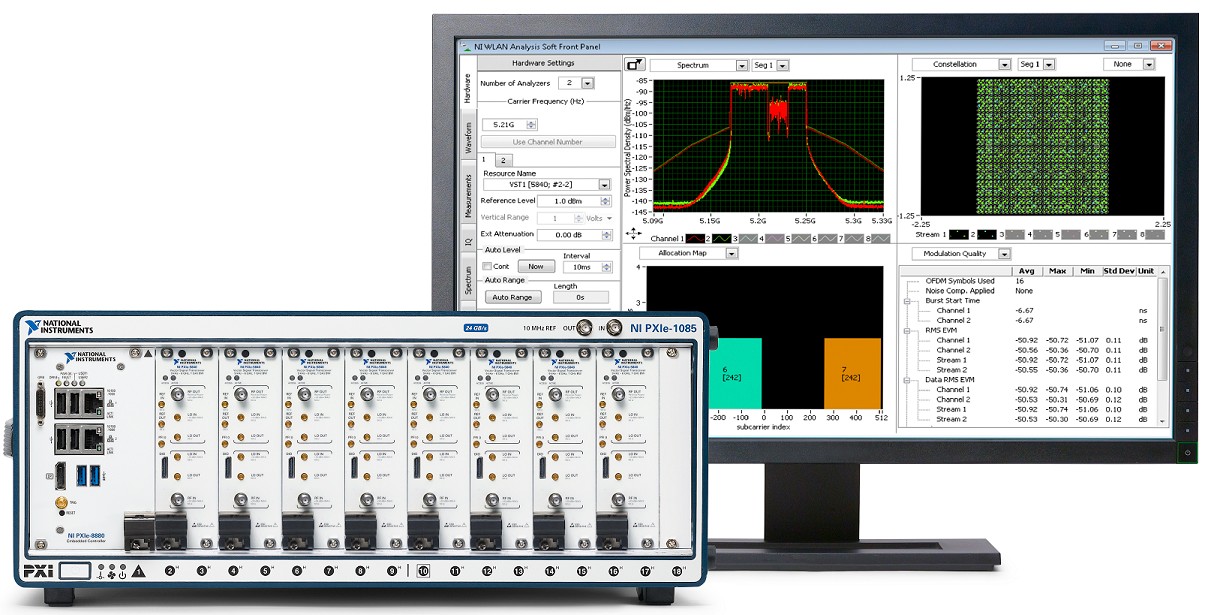
NI WLAN test systems combine an PXI Vector Signal Transceiver (VST) with RFmx WLAN to support generation and analysis of 802.11ax signals. The software supports waveforms ranging from BPSK (MCS0) to 1024-QAM (MCS10 and MCS11). In addition, NI’s VST hardware consistently delivers best-in-class EVM floor measurements for RF characterization and production needs.
Absolute and Relative Frequency Error
OFDMA systems have very high susceptibility to frequency and clock offsets. Consequently, 802.11ax Multi-user OFDMA performance demands extremely tight frequency synchronization and clock offset correction. This ensures that all STAs operate exactly within their allocated subchannels with minimal spectral leakage. Additionally, the strict timing requirements guarantee that all STAs will transmit simultaneously in response to the AP’s MU trigger frames.
In the case of 4G LTE systems, base stations have the advantage of GPS disciplined clocks to synchronize all associated devices. However, 802.11ax APs likely won’t have that luxury, and they will have to maintain system synchronization using their own built-in oscillators as the reference. STAs will then adjust their internal clock and frequency references by extracting offset information from the trigger frames that they get from the AP.
Frequency and clock offset testing of 802.11ax devices will involve the following tests:
- Absolute frequency error: the DUT sends 802.11ax frames and the test instrument measures the frequency and clock offset against a standard reference. This will be similar to what the current 802.11ac specification indicates, with limits around ±20ppm.
Figure 14. Simple setup for absolute frequency error measurement
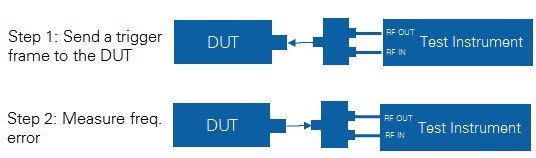
- Relative frequency error: this will test the ability of a non-AP STA participating in uplink multi-user transmission to align itself with the AP’s frequency. The test procedure goes in two steps. First, the test instrument sends a trigger frame to the DUT. The DUT adjusts itself based on the frequency and clock information it derives from the trigger frame. Then the DUT replies with frequency-corrected frames. The test instrument measures the frequency error of these frames. After carrier frequency offset and timing compensation, these limits will likely remain very strict around less than 350 Hz and ±0.4 µs relative to the AP’s trigger frame.
Figure 15. Setup for relative frequency error measurement
STA Power Control
Similar to the requirement of reduced frequency and clock errors, the power that an AP receives during uplink multi-user transmissions should not have large variations across all users. This requires that the AP controls the transmit power of each individual STA. The AP may use a trigger frame that contains transmit power information for each STA. Developers can test this functionality in two steps, in a way similar to the frequency error test.
Access Point Receiver Sensitivity
Testing the receiver sensitivity of 802.11ax APs presents an additional challenge, considering that the AP acts as the clock and frequency reference.Therefore, the test instrument has to lock on to the AP before sending packets to the AP for packet error rate sensitivity tests.
When the AP initiates by sending a trigger frame, the test instrument adjusts its frequency and clock to match the AP and then responds to the AP DUT with a predetermined number of packets with the expected configuration.
The challenge here has to do with the strict relative frequency error limits of 802.11ax. The test instrument has to derive very precise frequency and clock information from the trigger frames that the AP sends. It might be necessary to perform this calculation over multiple trigger frames to ensure proper frequency and clock synchronization. As a result, this procedure could add a significant delay to the test procedure.
One possible solution to speed up the test procedure is for the AP to export its clock reference, such that the test equipment could lock its clock to it. This avoids the initial synchronization procedure based on trigger frames and leads to faster AP receiver sensitivity test times.
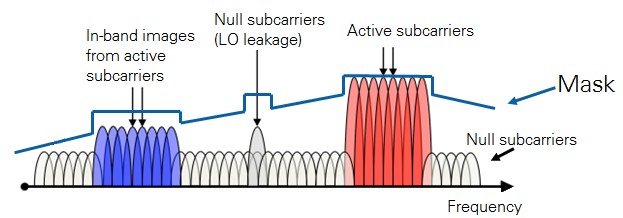
Uplink In-band Emissions
When STAs operate in MU-OFDMA mode they transmit up to the AP using the RU allocation that the AP determined. That is, STAs use only a portion of the channel. The 802.11ax standard might specify an uplink in-band emission test to characterize and measure the emissions that occur when the transmitter uses only a partial frequency allocation.
Figure 16. Potential uplink in-band emissions test mask
Multi-user and Higher Order MIMO
Testing 802.11ax devices with up to 8 antennas in MIMO operation can produce very different results than testing each signal chain individually and sequentially. For example, the signals from each antenna might interfere destructively with each other and affect power and EVM performance, with negative and potentially noticeable effects on the throughput.
Test instrumentation would have to support sub-nanosecond synchronization of the local oscillators for each signal chain to ensure proper phase alignment and MIMO performance over many channels. NI’s test solution, based on the NI VST, uses patented hardware and software technology to enable flexible massive MIMO configurations with up to 8, 16, or even 64 synchronized channels.
Conclusion
802.11ax promises to improve the average data throughput per user in dense environments by 4X. One of the biggest enablers of this efficiency is multi-user technology, both in the form of MU-MIMO and MU-OFDMA. This improvement in spectrum use in crowded environments will likely drive 802.11ax market adoption at faster rates than ever before. However, implementing this functionality will present a whole new set of challenges for the scientists, engineers, and technologists in charge of making these engineering marvels a reality.
NI’s flexible and modular platform offers high-performing hardware with clean oscillators and low EVM floor for 1024-QAM measurements with 4X closer subcarrier spacing. RFmx WLAN stays abreast of the latest developments of the nascent 802.11ax standard to help you design, characterize, validate and test your 802.11ax devices and be ready for the multi-user revolution.
About NI and the 802.11ax standard
RFmx WLAN and the PXI VST combine to deliver a modular and powerful test solution for 802.11ax devices. RFmx WLAN gives researchers, engineers and technologists the power and flexibility to generate and analyze a wide range of 802.11 waveforms, such as 802.11a/b/g/n/j/p/ac/ah/af. Now, with the measurement suite’s latest update targeting 802.11ax, these users can speed up development work on 802.11ax devices. The software supports key features of 802.11ax including narrower subcarrier spacing, 1024-QAM, and Multi-user OFDMA. The updated software also includes LabVIEW system design software example code to help engineers automate WLAN measurements quickly and easily.
Figure 17. NI 802.11ax 8x8 MIMO Test System with WLAN Measurement Suite and VSTs
Watch this video how to use the WLAN Test Toolkit and a PXI Vector Signal Transceiver (VST) to generate and analyze a 2x2 MIMO 802.11ax signal. PXI VSTs combine the functionality of a vector signal generator, vector signal analyzer, and user-programmable FPGA into a single device.
References
- [1] http://auto.ferrari.com/en_US/sports-cars-models/car-range/california-t/#specifications. Accessed 04/29/2016
- [2] https://newsroom.cisco.com/press-release-content?articleId=1741352. Accessed 05/01/2016
- [3] IEEE: IEEE 802.11-16/0024r1, Proposed TGax draft specification
- [4] IEEE 802.11-15/0132r16, Specification Framework Document