Wavelet-Based Peak Detection
Contents
- Identifying peaks and valleys using wavelet-based peak detection
- Wavelet-based peak detection using multiresolution analysis
- Determining the wavelet transform level to use
- Comparing the wavelet-based and curve-fitting-based methods
Peak detection is the process of finding local maxima and minima of a signal that satisfy certain properties. You can perform peak detection, such as threshold peak detection and curve-fitting-based peak detection, using LabVIEW.
The Advanced Signal Processing Toolkit, which is included in LabVIEW Professional, is a suite of VIs, libraries, software tools, example programs, and utilities for signal processing and analysis. This toolkit provides tools for wavelet analysis, time frequency analysis, and time series analysis, including the ability to perform peak detection using the WA Multiscale Peak Detection VI.
This document mainly describes wavelet-based peak detection. The wavelet-based peak detection method utilizes the inherent multiscale nature of wavelet analysis and is more robust and accurate than the threshold or curve-fitting-based peak detection method.
Identifying peaks and valleys using wavelet-based peak detection
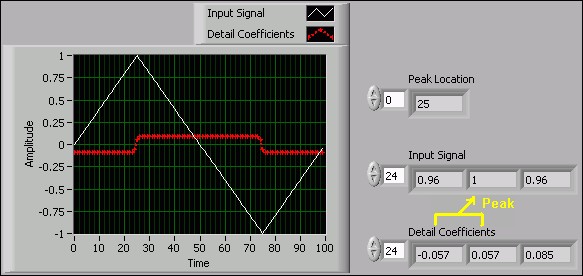
Wavelet analysis represents a signal using approximation coefficients and detail coefficients. A zero crossing in the detail coefficients usually corresponds to a peak or valley in the input signal, as shown in the following figure:
Figure 1: Corresponding zero crossings to signal peaks or valleys
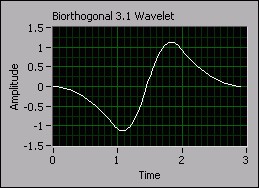
Although a wide variety of wavelets are available, not all are appropriate for wavelet-based peak detection. This document uses the biorthogonal 3.1 wavelet, as shown in the following figure, to perform wavelet-based peak detection.
Figure 2: Biorthogonal 3.1 wavelet
Wavelet-based peak detection using multiresolution analysis
Multiresolution analysis is useful for identifying peaks and valleys of noisy signals. This method makes wavelet-based peak detection more accurate and robust than threshold or curve-fitting-based peak detection methods.
Signals usually contain both low-frequency components and high-frequency components. Low-frequency components vary slowly with time and require fine frequency resolution but coarse time resolution. High-frequency components vary quickly with time and require fine time resolution but coarse frequency resolution. Therefore, a multiresolution analysis method is useful for analyzing a signal that contains both low- and high-frequency components.
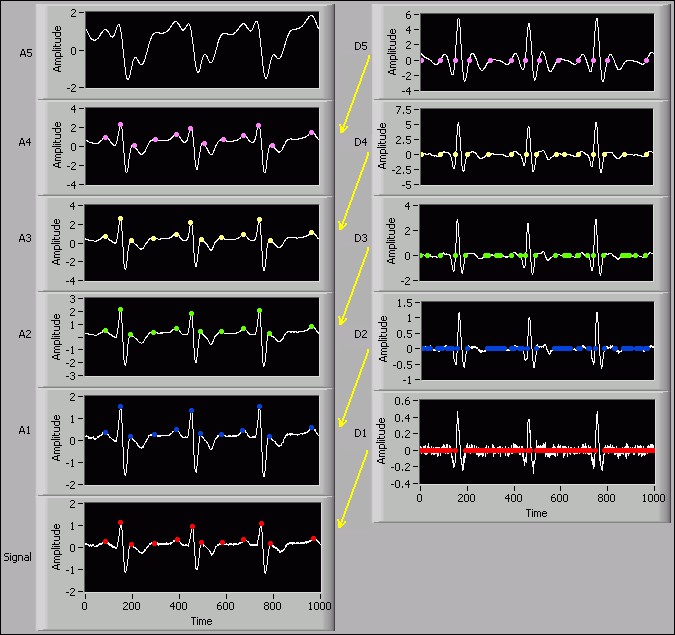
The multiresolution analysis method can help you recognize both the long-term trend and short-term variations of a signal. Information on the coarser resolution of a signal can help you locate the features, such as peaks, in which you are interested. Observation of the finer resolution levels can refine the gross features and provide more details. The following figure shows the multiresolution refinement process of the wavelet-based peak detection method.
Figure 3: The multiresolution process of wavelet-based peak detection
In this example, you perform five levels of undecimated wavelet transforms (UWT) on the input signal. The signal can be represented using the following equation:
Signal = A1 + D1
= A2 + D2 + D1
= ...
= A5 + D5 + D4 + D3 + D2 + D1
where A denotes the approximation coefficients and D denotes the detail coefficients.
After applying the UWT to the signal, the wavelet-based peak detection method first checks D5 for zero crossings, which correspond to the peaks in A4. Then, this method checks D4 for zero crossings. More zero crossings might exist in D4 than in D5 due to higher-frequency components or noise, so this method selects the zero-crossing points that are nearest to those in D5, which correspond to the peaks in A3. This method repeats the process until it reaches the finest scale in D1. The following figure shows the refinement process of the first detected peak.
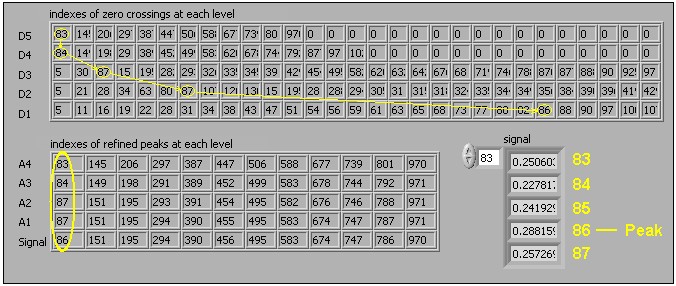
Figure 4: The refinement process of the first detected peak
In D5 of the previous figure, the first zero crossing is at index 83. In D4, the zero crossing nearest to 83 is 84. The refinement process repeats until the peak is refined to index 86 in D1. You can see from the Signal array that index 86 is indeed a local maximum.
Determining the wavelet transform level to use
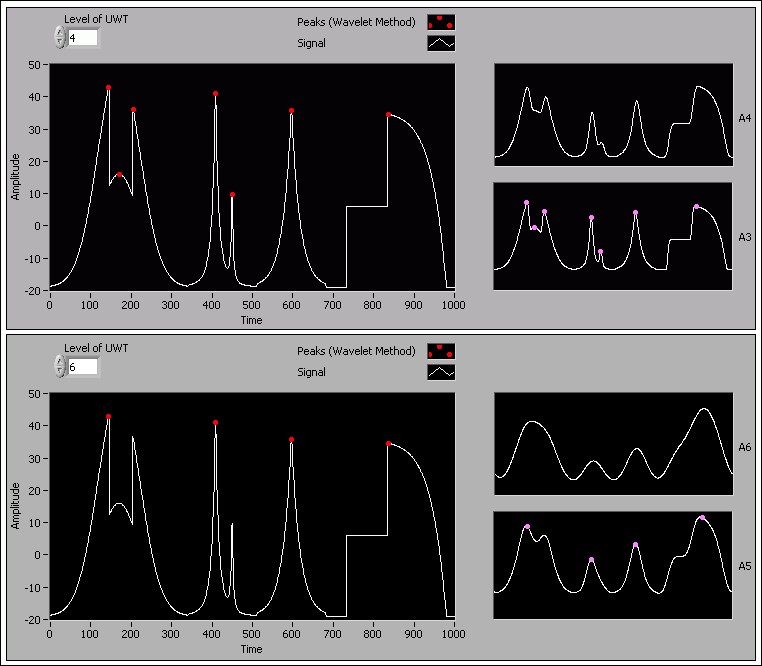
You can determine an appropriate level of wavelet transforms to find the peaks or valleys in an input signal. For noise-free data, a small level value is sufficient. For noisy data, you might need a large level value. When you use a large level value, you first need to check if the resulting peak locations and amplitudes at that level are what you expect. The following figure shows the effects of different wavelet transform levels.
Figure 5: Wavelet-based peak detection results at levels 4 and 6, respectively
In the previous figure, when Level of UWT is 4, the wavelet-based peak detection method identifies all the seven peaks in the input signal. When Level of UWT is 6, this method identifies only four peaks. The approximation signals at higher levels are smoother, and small peaks might disappear at higher levels due to the limited frequency bandwidth.
The wavelet transform level affects the number and location of the peaks or valleys in a signal. You can reduce noise or discard insignificant peaks by using a large level value. Conduct initial testing to determine the optimum level and check to see if the results are reasonable.
Comparing the wavelet-based and curve-fitting-based methods
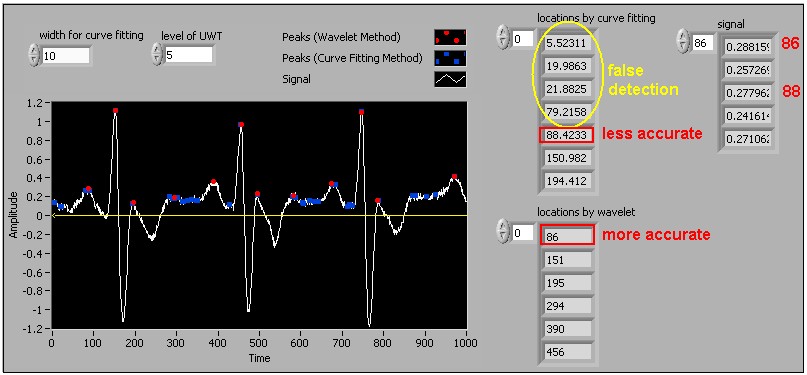
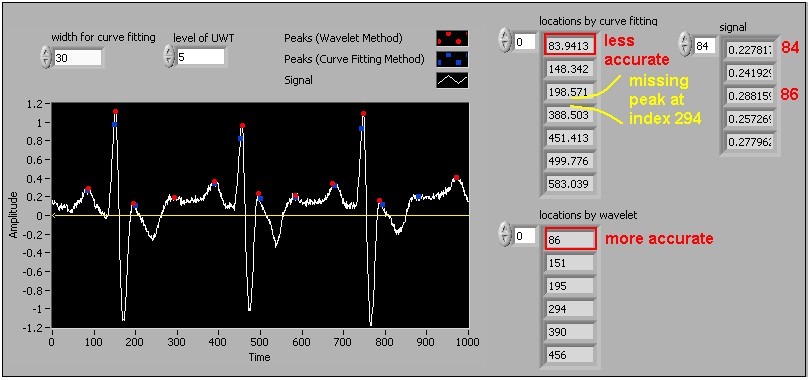
Figures 6a and 6b compare the wavelet-based and curve-fitting-based peak detection methods used to process an electrocardiogram (ECG) signal.
Figure 6a: Comparing curve-fitting-based and wavelet-based peak detection with width for curve fitting = 10 and level of UWT = 5
Figure 6b: Comparing curve-fitting-based and wavelet-based peak detection with width for curve fitting = 30 and level of UWT = 5
This example sets the level of UWT to 5. Notice that the wavelet-based method accurately identifies the peaks in the ECG signal with this value. However, the curve-fitting-based method is not as accurate as the wavelet-based method. When the width for curve fitting is small, this method returns false detections. When the width for curve fitting increases, the curve-fitting-based method fails to identify some real peaks. In both figures above, the wavelet-based method is more accurate than the curve-fitting-based method.
Refer to the LabVIEW Help for more information about approximation coefficients, detail coefficients, multiresolution analysis, and the UWT.