Analog Fundamentals
Overview
As part of the National Instruments Measurement Fundamentals Series, this set of tutorials helps you learn about a specific common measurement application topic through theory explanations and practical examples.
What You Learn
A wide range of systems and applications incorporate analog devices and signals, so advancing your analog fundamental knowledge is important for mastering many of today’s test and measurement applications. This set of analog tutorials provides you with essential information about analog circuits, ground loops, noise, sampling, windowing, isolation, and proper connection schemes for measurements.
Contents
- Basic Analog Circuits
- Sampling Quality
- Windowing: Optimizing FFTs Using Window Functions
- Dithering, Layout, and High-Quality Components: Tools to Decrease the Noise Floor
- Ground Loops and Returns
- High-Voltage Measurements and Isolation
- Low Frequency and DC Measurements
Basic Analog Circuits
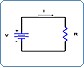 | Review basic analog circuit fundamentals through this tutorial, which covers analog circuit concepts explaining Ohm’s law, capacitance calculations, inductance calculations, series and parallel configurations for capacitance and inductance, and RC filters. View Comprehensive Tutorial >> |
Sampling Quality
 | Learn sampling quality basics such as resolution, measurement sensitivity, accuracy, precision, noise, and noise reduction strategies. View Comprehensive Tutorial >> Learn more about settling time >> |
Windowing: Optimizing FFTs Using Window Functions
 | Investigate windowing and ways you can use window functions to minimize spectral leakage effects. Also review different window functions and see how to implement them in the National Instruments LabVIEW graphical development environment. View Comprehensive Tutorial >> |
Dithering, Layout, and High-Quality Components: Tools to Decrease the Noise Floor
 | Scientists and engineers taking analog measurements often use the term “noise floor,” which is often misunderstood and, as a result, not dealt with correctly. Reduce the noise that occurs on your measurements by obtaining a firm understanding of the noise floor, its components, and what you can do to decrease it in your measurement system. View Comprehensive Tutorial >> |
Ground Loops and Returns
 | Gain a better understanding of the benefits of proper grounding by studying the different types of signal sources and measurement systems. Then review different configurations to match a signal source with its best measurement system for minimal noise and error. View Comprehensive Tutorial >> |
High-Voltage Measurements and Isolation
 | Learn about the types of input configurations available on data acquisition devices and the best ways to choose and use the configurations for your applications. Review interference noise pickup mechanisms and strategies to minimize interference noise by proper cabling and shielding. View Comprehensive Tutorial >> |
Low Frequency and DC Measurements
 | Review the basics of low frequency and DC measurements such as definitions and detailed explanations of concepts including common mode rejection ratio (CMRR), AC RMS measurement fundamentals, resistance measurement, current measurement, and crest factor. View Comprehensive Tutorial >> |
Related Links:
Return to the Measurement Fundamentals Main Page