From Friday, April 19th (11:00 PM CDT) through Saturday, April 20th (2:00 PM CDT), 2024, ni.com will undergo system upgrades that may result in temporary service interruption.
We appreciate your patience as we improve our online experience.
From Friday, April 19th (11:00 PM CDT) through Saturday, April 20th (2:00 PM CDT), 2024, ni.com will undergo system upgrades that may result in temporary service interruption.
We appreciate your patience as we improve our online experience.
This tutorial recommends tips and techniques for using a NI digital multimter (DMM) to build the most accurate measurement system possible. Learn how the PXIe-4082 DMM can operate as a 6½-digit DMM, a fully isolated, high-voltage digitizer capable of acquiring waveforms at sample rates up to 1.8 MS/s at ±300 V input, and an LCR meter measuring inductance and capacitance. This section of the tutorial covers the topics below.
The PXIe-4082 uses a 2-wire, multitone, constant current technique to measure impedance. When you apply a multitone constant current source (Isrc) to the device under test (DUT), the PXIe-4082 measures the fundamental and third harmonic of the voltage waveform.
Figure 1. Measuring the Fundamental and Third Harmonic of a Voltage Waveform
When the current and voltage are known, the NI 4082 calculates the capacitance or inductance using fast Fourier transform (FFT) peak analysis. If the residual series impedance (Zs) and the stray parallel admittance (Yp) introduce a significant error in the measurement, the PXIe-4082 can measure the magnitude of the error and reduce it using compensation techniques.
Capacitive and inductive loads oppose the flow of alternating currents. This opposition is expressed as impedance at a given frequency. The effect of a real-world impedance load is observed as an attenuation of the signal and a phase shift. Because of the nature of the impedance, it is denoted as a vector whose angle is the same as the phase angle between voltage and current, and the magnitude of the impedance is the same as the quotient between the voltage and current magnitudes, as follows.
Note: Bold values denote vector quantities or complex numbers.
Z = V/I
Numerically, the impedance vector is represented as a complex number either in polar form (magnitude and phase) or rectangular form (real and imaginary). The following equation expresses impedance in rectangular form:
Z = R + jX
where R and X are resistance and reactance, respectively. When X = 0, the load is purely resistive; when R = 0, the load is purely reactive. For capacitors, the reactance can be expressed as follows:
Xc = –1/(2πfCs)
For inductors, the reactance can be expressed as follows:
XL = 2πfLs
In real-world applications, loads are neither purely reactive nor purely resistive. However, they can be easily modeled either as a series or parallel combination of a resistive and a reactive load using the formulas above.
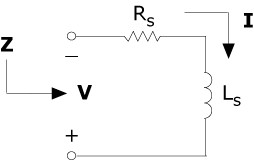 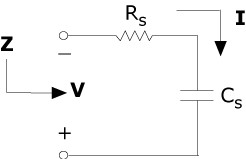 |
Figure 2. You can easily model loads either as a series or parallel combination of a resistive and a reactive load using the formulas above.
To simplify mathematical manipulation, calculation, and analysis, it is sometimes convenient to express the impedance as its reciprocal quantity, or admittance. Admittance is defined as
Y = 1/Z = I/V
and can be written as
Y = G + jB
where G and B are the rectangular (real and imaginary) components, known as conductance and susceptance, respectively. The conductance G is the reciprocal of the parallel resistance, as follows:
G = 1/RP
The susceptance for capacitors is expressed as follows:
BC = 2fCP = 1/XC
The susceptance for inductors is expressed as follows:
BL = 1/2fLP = 1/XL
In general, it is mathematically easier to manipulate parallel loads as admittances and series loads as impedances.
Figure 3. It is mathematically easier to manipulate parallel loads as admittances and series loads as impedances.
At times, you may need to obtain the result as a series model or as a parallel model. The parallel resistance is typically larger than the series resistance. To measure small reactive values, such as high-valued capacitors and low-valued inductors, it is preferable to use the series model because the series resistance is more significant than the parallel resistance. When measuring large reactive values, such as high-valued inductors or low-valued capacitors, it is preferable to use the parallel model.
Type of Measurement
| Range
| Impedance
| Model
|
|---|---|---|---|
C
| >100 uF
| <10 Ω
| Series
|
C
| 10 nF to 100 uF
| 10 Ω to 10 kΩ
| Series or parallel
|
C
| <10 nF
| >10 kΩ
| Parallel
|
L
| <1 mH
| <10 Ω
| Series
|
L
| 1 mH to 1 H
| 10 Ω to 1 kΩ
| Series or parallel
|
L
| >1 H
| ≥1 kΩ | Parallel
|
| Note: Impedance values are calculated at the test frequency used on an PXIe-4082 at each specified range. |
Table 1. Capacitor (C) and Inductor (L) Measurements and Their Preferred Models
Capacitors
A capacitor is an electronic component that is capable of storing energy as charge. Each capacitor consists of two plates of conductive material that are separated by a dielectric, which could be air, paper, plastic, oxide, or any other type of insulator. The dielectric constant, or K, of an insulator represents its ability to store charge. Table 2 shows the K values for different dielectric materials.
Dielectric
| Dielectric Constant (K)
|
|---|---|
Vacuum
| 1
|
Air
| 1.0001
|
Teflon
| 2.0
|
Polypropylene
| 2.1
|
Polystyrene
| 2.5
|
Polycarbonate
| 2.9
|
Polyester
| 3.2
|
FR-4
| 3.8–5.0
|
Glass
| 4.0–8.5
|
Mica
| 6.5–8.7
|
Ceramics
| 6 to several thousand
|
Aluminum oxide
| 7
|
Tantalum oxide
| 11
|
Table 2. K Values for Different Dielectric Materials
The electrical properties of insulators show variability with factors such as temperature, frequency, voltage, and humidity. This variability and the mechanical construction of the capacitor create a less than ideal device. A better representation of real-world capacitors is shown in the equivalent model in Figure 4, which can help you understand the different parasitic elements that are present in a real-world component. These parasitic elements impact the capacitor impedance at different test frequencies.
Figure 4. A Model of Different Parasitic Elements in a Real-World Component That Can Impact the Capacitor
The parallel resistance, Rp, is usually a large value, and its effect is significant only when measuring capacitors with small values. The equivalent series resistance, Rs, although a small value, is important in capacitors with large values, where the impedance is small compared to Rs and where high power is dissipated. The series inductance, Ls, represents the total inductance and capacitance roll-off at higher frequencies. At low frequencies, capacitance varies with frequency and the test signal level, due to changes in the dielectric properties. The Figure 5 graph shows a 2.2 µF, 100 V aluminum electrolytic capacitor measured at different frequencies. The error is referenced to the measurement using a 1 Vrms AC test signal at 1 kHz.
Figure 5. A 2.2 µF, 100 V Aluminum Electrolytic Capacitor Measured at Different Frequencies
These factors cause capacitors to have different values under varying conditions of temperature, frequency, and signal level.
An inductor is an electronic component that is capable of storing energy as current. Each inductor consists of a conductive coil that can be wrapped without a core or around a magnetic material. The permeability of the core material is a measure of the intensity of the magnetic field that can be induced in it. The electrical properties of the cores show variability with factors such as temperature, frequency, current, and so on. This variability and the mechanical construction of the inductor create a less than ideal device. A better representation of real-world inductors is shown in the equivalent model in Figure 6, which can help you understand the different parasitic elements that are present in a real-world component. These parasitic elements impact the inductor impedance at different test frequencies.
Figure 6. A Model of Different Parasitic Elements in a Real-World Component That Can Impact the Inductor
The series resistance, Rs, represents the resistive losses in the conductor. The parallel capacitance, Cp, is the equivalent capacitive effect between the turns of the coil, and the parallel resistance, Rp, is the sum of all losses attributable to the core material. Air cores require many more turns in the coil to achieve high-inductance values. Thus, air cores are often impractical for applications, due to their large size and weight. Also, air cores usually have a large winding capacitance and a series resistance with a high-inductance value. Not all parasitics affect the value of the inductor, but some parasitics are more prominent than others, depending on the construction of the coil, the geometry of the inductor, the gauge of the wire, and the characteristics of the core. The value of the inductor and the magnitude of each type of parasitic in relation to the other types of parasitics determine the frequency response. The geometry of some components can increase the sensitivity of the components to external factors, and this increased sensitivity can affect the value of the inductor. Open flux inductors are more sensitive to metallic materials that are in close proximity because such materials modify the magnetic field. Toroidal inductors keep the flux inside the core and are less sensitive to external conductors in close proximity. Refer to Figure 7 to view the flux associated with these types of inductors:
Figure 7. Types of Inductor Flux
In Figure 8, a 5 mH air-core inductor is measured over different frequencies. The error is referenced to the measurement with a test signal of 1 Vrms at 1 kHz. This type of inductor has a high degree of winding capacitance due to the size and number of turns required for its construction. Therefore, this type of inductor measures as if there were a strong variation of inductance with frequency.
Figure 8. A 5 mH Air-Core Inductor Measured over Different Frequencies
Some ferrite cores are expected to vary greatly with the test signal level. In Figure 9, a 100 uH ferrite-core inductor is tested at different test signal levels. The error is referenced to the measurement with a test signal of 1 mArms at 1 kHz.
Figure 9. A 100 uH Ferrite-Core Inductor Tested at Different Test Signal Levels
All of these factors can combine and cause inductors to have different values under varying conditions of temperature, frequency, and signal level.
PXIe-4082 DMMs use an AC current source as excitation for capacitance and inductance measurements. The current waveform is a very stable, harmonically limited square wave. The measurement method extracts multiple-tone information contained in the test signal to find the capacitance or inductance of the device under test. The frequency and level of the test signal and the tones extracted from it are shown in tables 3 and 4:
Capacitance
| ||||||
|---|---|---|---|---|---|---|
Range
| Fundamental
| Third Harmonic
| Effective Test Signal
| |||
Frequency
| Current
| Frequency
| Current
| Frequency
| Current
| |
| 300 pF | 1 kHz
| 0.5 µA
| 3 kHz
| 0.16 µA
| 3 kHz
| 0.16 µA
|
| 1 nF | 1 kHz
| 1 µA
| 3 kHz
| 0.33 µA
| 3 kHz
| 0.33 µA
|
| 10 nF | ||||||
| 100 nF | 1 kHz
| 10 µA
| 3 kHz
| 3.3 µA
| 3 kHz
| 3.3 µA
|
| 1 uF | 1 kHz
| 100 µA
| 3 kHz
| 33 µA
| 1 kHz
| 100 µA
|
| 10 uF | 1 kHz
| 1 mA
| 3 kHz
| 330 µA
| 1 kHz
| 1 mA
|
| 100 uF | 91 Hz
| 1 mA
| 273 Hz
| 330 µA
| 91 Hz
| 1 mA
|
| 1,000 uF | ||||||
| 10,000 uF | ||||||
Inductance
| ||||||
|---|---|---|---|---|---|---|
Range
| Fundamental
| Third Harmonic
| Effective Test Signal
| |||
Frequency
| Current
| Frequency
| Current
| Frequency
| Current
| |
| 10 uH | 10 kHz | 1 mA | 30 kHz | 330 µA | 30 kHz | 330 µA |
| 100 uH | ||||||
| 1 mH | 1 kHz
| 1 mA
| 3 kHz
| 330 µA
| 3 kHz
| 330 µA
|
| 10 mH | 1 kHz
| 10 µA
| 3 kHz
| 3.3 µA
| 3 kHz
| 3.3 µA
|
| 100 mH | 91 Hz
| 100 µA
| 273 Hz
| 33 µA
| 273 Hz
| 33 µA
|
| 1 H | 91 Hz
| 10 µA
| 273 Hz
| 3.3 µA
| 273 Hz
| 3.3 µA
|
| 5 H | 91 Hz
| 1 µA
| 273 Hz
| 0.33 µA
| 273 Hz
| 0.33 µA
|
Tables 3 and 4. The Frequency and Level of the Test Signal and the Tones Extracted from It
The digitizer measures the DUT impedance at two frequencies (tones). From these two measurements, the losses are calculated (front-end, cabling, and DUT). Using the calculated losses, the software computes the capacitance or inductance at one of the two frequencies (effective frequency). The effective test signal is included as a reference. It is the signal that yields a comparable capacitance or inductance value if measured with the single-tone measurement technique. Due to the parasitics and materials used in the construction of real-world components, the measured capacitance or inductance value can differ from one instrument to another. When measuring capacitors with better dielectric properties, you observe much smaller reading differences between various instruments. This observation also applies to inductors with better magnetics. Table 5 shows some examples of dielectrics with good and poor frequency characteristics.
Dielectrics with Good Frequency Characteristics
| Dielectrics with Poor Frequency Characteristics
|
|---|---|
| Teflon Mica Polypropylene Polycarbonate Ceramic COG | Tantalum oxide Aluminum oxide Ceramic Y5U |
Table 5. Examples of Dielectrics with Good and Poor Frequency Characteristics
Due to the amount of magnetization current required, you can see an increase in sensitivity to frequency changes and other dependency factors in inductors with cores of larger dimensions, such as those used in transformers and power inductors.
Temperature can have a large impact on the DUT impedance. Usually, capacitors have large temperature coefficients (5 to 80 percent variation over the entire temperature range, depending on the capacitor used) except for ceramic COG capacitors, which can exhibit only a 0.003%/°C variation. Inductors, especially those with non-air cores, may vary largely with temperature. Ambient and DUT temperature drifts (due to handling, for instance) may introduce error into the measurement. Control ambient temperature changes to reduce errors.
To reduce variations on the system parasitics, NI recommends using coaxial cable or shielded twisted pairs, with the shield used as the current return path and connected to the LO input of the DMM. This configuration makes the OPEN/SHORT compensation more practical and helps to reduce the noise pickup. For manual probing of surface mount parts, you can use a pair of tweezers. The PXIe-4082 DMM can compensate for the impedance introduced by the test fixtures. Refer to the OPEN/SHORT Compensation section below for more information. Reduce the mechanical variations (for example, movement or flexing of cables, or changing fixturing) between two consecutive measurements to maintain repeatability. Use a high-quality cable, such as a Belden 83317, available at belden.com. NI recommends cables with Teflon, polypropylene, or polyethylene insulation. For more information about cabling requirements, refer to Interconnects and Cables. Very good performance has been achieved using up to 25 ft of this cable in both capacitance and inductance measurements by performing OPEN/SHORT compensation prior to the measurement.
To minimize noise pickup, keep cables, the setup, and the DUT away from any electromagnetic noise sources such as motors, transformers, and cathode ray tubes (CRTs). Avoid frequency sources around 91 Hz, 1 kHz, 10 kHz, and the respective harmonics because these frequencies are the frequencies of the excitation currents used by an NI 4082. Use shielded cable (BNC connectors and coaxial cable are recommended) for cabling and for connecting the external conductor to the LO input of the DMM.
In most practical applications, the DMM is connected to the DUT with switches and/or fixtures. These switches and fixtures can introduce undesired errors into the measurement. Compensation minimizes the errors between the PXIe-4082 DMM and the DUT.
Compensation consists of measuring the error and applying the measured error to the actual measurement to correct and minimize the errors introduced by the test system. The compensation functions must be set before taking any measurement at a specified function and range. Any change in range or function defaults the compensation type to none. Therefore, you must calculate these values again. To provide maximum flexibility in the test system, the compensation values are returned by the API. You can manipulate, store, and load these values for high-channel-count systems.
To perform OPEN compensation for capacitance and inductance measurements, complete the following steps:
To perform SHORT compensation for capacitance and inductance measurements, complete the following steps:
To perform OPEN and SHORT compensation for capacitance and inductance measurements, complete the following steps:
Note: Due to ambient temperature variations and other environment changes, such as humidity, you may need to perform OPEN and SHORT compensation at least once a day. When using a switching system, verify that the OPEN and SHORT measurements on the reference channel closely match the measurements on the rest of the channels you are compensating. If this compensation method does not meet your error budget requirements, you must perform OPEN and/or SHORT compensation on the same channel used to take the DUT measurements.
To test some polarized components, such as electrolytic and tantalum capacitors, you may prefer to use only positive voltages. During normal operation, the AC current source swings negative 50% of the time, which results in an inverse polarization of the capacitor under test. To prevent this inverse polarization, you can apply a DC bias to prevent the voltage across the part from becoming negative.
Note: When DC bias is turned ON, the high potential appears on the HI terminal. Ensure that the component is polarized correctly by connecting the negative terminal of the component to the LO terminal.
The DC bias voltage is a fixed value and can only be turned on and off. The nominal voltage value is 0.45 V and can be used for any capacitance range. The default setting is OFF.
NI also offers a combination source measure unit and LCR Meter that you can use to measure and test the inductance, capacitance, and resistance (LCR) of electronic equipment. The PXI LCR Meter provides femtofarad-class capacitance measurements and femtoampere-class current measurements in a single-slot PXI form factor.