From Friday, April 19th (11:00 PM CDT) through Saturday, April 20th (2:00 PM CDT), 2024, ni.com will undergo system upgrades that may result in temporary service interruption.
We appreciate your patience as we improve our online experience.
From Friday, April 19th (11:00 PM CDT) through Saturday, April 20th (2:00 PM CDT), 2024, ni.com will undergo system upgrades that may result in temporary service interruption.
We appreciate your patience as we improve our online experience.
For more than 30 years, NI PC-based data acquisition (DAQ) devices have set the standard for accuracy and performance. Measurement accuracy is arguably one of the most important considerations in designing any data acquisition application. Yet equally important is the overall performance of the system, including I/O sampling rates, throughput, and latency. For most engineers and scientists, sacrificing accuracy for throughput performance or sampling rate for resolution is not an option. Through years of experience, NI has developed several key technologies to maximize the absolute accuracy of your measurements while delivering industry-leading performance in PC-based data acquisition from PCI to PXI and USB to wireless.
NI-MCal is a software-based calibration algorithm that generates a third-order polynomial to correct for the three most common sources of measurement error: offset, gain, and nonlinearity. Most data acquisition devices today perform some form of self-calibration during which onboard voltage and ground references are used to determine the offset and gain errors introduced by the analog-to-digital converter (ADC). However, many data acquisition vendors overlook the fact that an ADC is a nonlinear system. Failing to account for this can introduce significant errors in a measurement, especially at the maximum and minimum measurement ranges of the device.
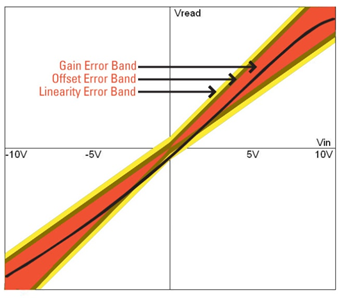
Figure 1. In addition to correcting for gain and offset errors, NI-MCal uses an advanced software algorithm to correct for the nonlinearities inherent to every ADC.
NI-MCal uses software to characterize nonlinearity in the ADC, generating a third-order polynomial to accurately translate the digital output of the ADC into voltage data. Specifically, NI-MCal “smooths out” the transfer curve of the ADC using a dithering and averaging technique, and linearizes the ADC transfer function through a set of third-order polynomial coefficients. Each time self-calibration is performed, NI-MCal repeats this procedure for each input range of the data acquisition device and stores the results in onboard EEPROM. Every channel in a scan list returns calibrated data, even if they are at different input ranges.
After the ADC, the programmable gain instrumentation amplifier (PGIA) is the second-most important piece of a data acquisition device. The PGIA delivers a scaled voltage signal to the ADC using different gain settings to maximize the resolution of the data acquisition device. Most off-the-shelf PGIAs are not optimized for data acquisition applications, because their settling times are too long. Settling time is the amount of time required for a signal that is being amplified to reach a specified level of accuracy. This is a critical specification when scanning multiple channels at varying voltage levels with a single device, because a shorter settling time leads to faster sampling rates without sacrificing accuracy.
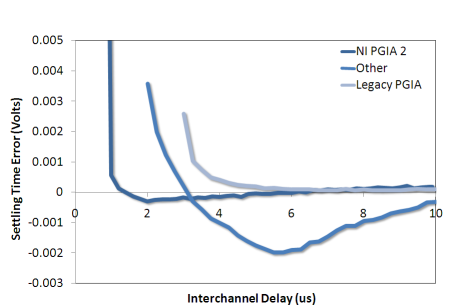
Figure 2. The NI-PGIA 2 demonstrates significantly better settling times over the legacy NI-PGIA and an off-the-shelf PGIA following a 20 V step between two adjacent channels on a data acquisition device.
The NI-PGIA 2 custom amplifier design on NI M Series devices incorporates a fully balanced signal path paired to the ADC. NI-PGIA 2 technology improves accuracy and increases performance by minimizing settling time and maintaining the specified resolution even at the maximum sampling rate of the device. Figure 2 above shows the high-speed NI-PGIA 2 settling to virtually zero error in 1.5 µs following a 20 V step (worst-case scenario).
Watch a video of how easy it is to take a measurement with a USB-based DAQ device
Many National Instruments DAQ devices include varying levels of electrical isolation to improve measurement accuracy and device performance. In the context of a measurement system, “isolation” means to electrically and physically separate sensor signals, which can be exposed to high-voltage transients and noise, from the measurement system’s low-voltage backplane. Isolation offers many benefits including protection for expensive equipment, the user, and data from harmful transient voltages; improved noise immunity; ground loop removal; and increased common-mode voltage rejection.
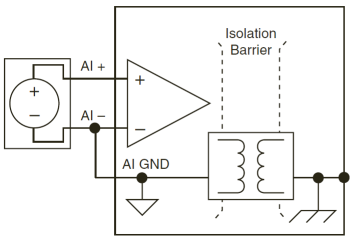
Figure 3. Isolation separates potentially hazardous signals from the low-voltage backend of a measurement system, and in doing so provides protection and improves noise immunity.
Isolated National Instruments DAQ devices provide separate ground planes for the analog and/or digital front end(s) and the device backplane to separate the sensor measurements from the rest of the system. The ground connection of the isolated front end is a floating pin that can operate at a different potential from the earth ground. Any common-mode voltage that exists between the ground and the measurement system ground is rejected (within the devices working voltage specification). Isolation also prevents ground loops from forming, helping reduce noise in the measurement signals. DAQ devices may be isolated on a per channel basis, as groups of channels, or as a complete system.
Recognizing the diversity of measurement applications, National Instruments approaches data acquisition independent of specific PC bus technologies. You can use the same NI-DAQmx API for communicating across PCI, PCI Express, PXI, PXI Express, USB, Ethernet, and Wi-Fi. Because each of these buses has different portability, throughput, and latency capabilities, NI signal streaming technology abstracts the complexity of programming these different architectures from the user. For example, NI signal streaming overcomes the lower throughput and higher latency associated with USB transfers to make bidirectional waveform streaming possible for a cabled USB DAQ device.
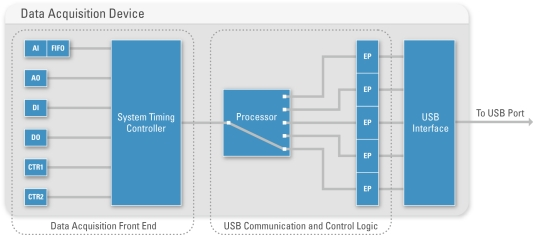
Figure 4. NI signal streaming for NI USB DAQ devices includes custom hardware and software interfaces for streaming continuous, bidirectional waveform data across the bus.
The same technology developed for USB is replicated across other instrumentation buses as well, including Ethernet and IEEE 802.11 (Wi-Fi). The result is that you can repurpose an application developed for a PCI DAQ device (even a high-speed application) to instead use a USB or wireless DAQ device without making any changes to the software. Thus, National Instruments DAQ performance is independent of the particular bus in use.